En tout premier, je dois remercier toutes les personnes qui ont souffert il y a dix ans lors de la première mouture du présent ouvrage, parmi lesquelles le regretté Edouard Parmelan, patience et perfectionnisme alliés à un savoir immense pour quelqu’un d’aussi jeune.

D’autre part, je dois remercier Alick Mouriesse de m’avoir permis de reprendre ce livre pour l’éditer réellement et tout ceux qui m’ont poussé à saisir l’occasion qui m’était proposée, parmi lesquels mon épouse Virginie et Marianne Belis, également écrivain et professeur à SupInfo.

Pour réaliser la première version, il m’a fallu trois ans de travail nocturne, j’ai épuisé l’amitié d’au moins une dizaine de lecteurs patients et j’ai fini par m’endormir au volant de ma voiture.

Cette fois-ci, le travail aura duré moins de deux mois et aura été beaucoup plus gratifiant. J’ai rajouté des exemples en Java quand cela était possible et je me suis réconcilié avec le paradigme objet. J’espère que vous aurez du plaisir à le lire, car j’en ai eu à l’écrire. J’espère aussi stimuler des réflexions.

1 Introduction

Il est ici question d’une promenade dans l’univers de la programmation qui nous permette de nous affranchir des langages. Je voudrais promouvoir un certain art de l’élaboration des algorithmes qui reste indépendant de son mode d’expression. Il est vrai que certains langages imposent certaines acrobaties de par leurs limitations syntaxiques. Ce livre est né des questions de mes élèves qui s’intéressaient moins aux solutions qu’aux moyen d’y parvenir. Comment fait-on pour résoudre un problème informatique ? Y a-t-il des recettes de cuisines pour trouver un algorithme ?

Le titre fait référence à la distillation qui permet d’atteindre le produit concentré. Nous utiliserons ici des exemples dans plusieurs langages différents pour ne pas être emprisonné par la forme et mieux sentir le fond. J’espère donner envie à certains de feuilleter les livres qui m’ont aidé, notamment ceux de Donald Knuth, Robert Sedgewick ou Alfred Aho et Jeffrey Ullman.

Afin de mieux cerner notre propos, voici une petite histoire de l’informatique revue et corrigée par un révisionniste mal intentionné^¹ :

A l’aube de l’humanité, après quelques « détails » de l’évolution darwinienne^² comme la découverte du feu et de la cornemuse, l’homo sapiens sapiens^³ finit par inventer l’ordinateur^⁴. Malheureusement pour les pionniers de la programmation, la science des ordinateurs n’avait pas bénéficié du passage d’une équipe de « Bourbakistes » (les gens qui ont inventé les « maths modernes » en formalisant tout à outrance) pour formaliser tout cela. La technologie progressait à une grande vitesse et il y avait de nombreux foyers de développement de la maladie informatique. Résultat, c’était la tour de Babel. Chacun venait mettre sa pierre à l’édifice en décrétant détenir la vérité universelle.

Quelques années plus tard, quelques grands hommes, des Knuth, Wirth et autres précurseurs vinrent avec des outils de formalisations qui pourraient sembler archaïques aujourd’hui, mais qui firent reculer les frontières de l’inconnu. On mit alors des étiquettes sur les objets informatiques.

Le début fut douloureux avec des machines habitant dans des bâtiments spéciaux maintenus à 70° Kelvin. Les données étaient stockées dans des rubans magnétiques ou des cartes perforées, les registres étaient en nombre très limités et le temps de calcul très long. La programmation était un art délicat où le moindre bit devait être exploité au mieux. Evidemment, le type de problème que nous rencontrons aujourd’hui est complètement différent car, contrairement à l’époque, maintenant, le temps de calcul est infiniment moins cher que le temps de programmation.

Puis dans les années 70, il y eu une sorte d’explosion : chaque projet créait son propre langage de « quatrième génération », chacun réinventait le thermomètre de son côté, lui trouvait un nom différent pour faire face à la concurrence. Globalement, c’est alors que naquit la possibilité de faire n’importe quelle monstruosité technologiquement nulle et de la vendre comme étant le stade ultime de l’application informatique^⁵.

A l’aube du troisième millénaire, les contrats ont des clauses de pénalités non libératoires, les avocats traînent derrière chaque informaticien et les utilisateurs commencent à se regrouper pour entarter les responsables de cet état de fait. Bref, on attend des résultats, même si certains grands éditeurs de logiciels continuent à livrer des versions bêta en tant que produits finis…

Fin de l’histoire et début des problèmes.

Nous n’en sommes encore qu’au début et nous manquons de formalismes véritablement consensuels. Pourtant, il existe plusieurs points de vue permettant de décrire nos données et nos traitements de manière plus ou moins unitaire, les types de données abstraits par exemple ou les « design patterns » chers aux partisans de l’objet.

Bref, nous voilà contraints à un certain professionnalisme dans notre travail de développement.

1.1 Encore un livre d’algorithmique ?

Et oui, des exemples et de la méthodologie de développement. Il s’agit de rassembler les quelques algorithmes qui sont censés former la culture de tous les développeurs et de donner quelques indications pour en construire de nouveaux. J’espère aussi donner un savoir faire pratique pour l’optimisation du travail du développeur. J’entend par là l’optimisation du code mais aussi, l’optimisation du temps de développement et de la qualité de ce qui est produit.

C’est en même temps un compte rendu d’une dizaine d’années passées à encadrer les travaux pratiques d’élèves ingénieurs. Je vais montrer des exemples dans divers langages informatiques dans l’espoir d’en faire une pierre de Rosette des langues informatiques^⁶.

Au passage, sans citer tous les livres qui m’ont influencé, j’aimerai quand même m’arrêter sur un livre qui m’a beaucoup changé et motivé : « Essentials of Programming Languages » de Daniel P. Friedman, Mitchell Wand et Christopher T. Haynes. Outre les nombreux exemples que j’ai pillés sans vergogne^⁷ pour mes cours, j’y ai trouvé quelques perles de sagesse informatique dont la préface de Hal Abelson^⁸. Il nous explique que tout programme peut être vu comme un interprète qui traduit le langage des données dans le langage du résultat. Il va même jusqu’à dire que sans maîtriser les interprètes^⁹, on peut devenir un bon programmeur, mais on ne peut jamais devenir un maître^¹⁰.

Visualisons donc tous les programmes comme traduisant des données en résultats. Le problème clef apparaît maintenant : décrire le langage de l’information. Tout le monde ne dispose pas de moyens pour décrire le langage des données et des résultats sous forme d’une quelconque grammaire ou de classes d’objets.

C’est là que peuvent intervenir les Types de Données Abstraits. En 1992, j’ai dirigé un ensemble d’étudiants sur un problème difficile pour eux à priori. Nous avons ensemble, construit une pyramide de trois ou quatre types abstraits qui nous permettaient de décrire les différentes formes successives de l’information, tout en permettant des démonstrations de propriétés mathématiques du résultat, sans avoir écrit une ligne de code. Et lors de l’implantation réelle, le programme s’est concrétisé correctement pour la totalité des élèves (cf. section 6.1.1). L’intérêt de la méthode ne réside pas seulement dans la simplicité des étapes de programmation, mais dans leur accessibilité à tous.

Les étudiants avaient énormément de facilité à communiquer leurs résultats partiels et à les mettre en commun pour améliorer leurs propositions.

On peut aussi formaliser avec UML ou Merise, mais on met alors l’accent sur la structure et non sur le traitement. Ce qui me paraît aujourd’hui le plus prometteur, c’est l’utilisation des « Design Patterns » qui permettent de regrouper tous les traitements informatiques en quelques six ou sept modèles connus pour lesquels le travail a déjà été fait. Le programmeur n’intervient alors que sur les particularités très spécifiques de son problème. On évite ainsi d’inventer l’eau chaude à chaque nouveau projet.

Mais pour pouvoir utiliser tous ces beaux modèles, il est nécessaire de connaître un petit peu la structure sous-jacente et c’est là qu’intervient ce livre.

1.2 Mais à qui s’adresse ce livre ?

Evidemment, il s’adresse à des programmeurs essentiellement, mais aussi à ceux qui les encadrent ou les forment. Il devrait y avoir suffisamment d’exemples pour permettre de comprendre ou même d’expliquer ce qu’on a compris.

Notez qu’il y a quelques pré requis techniques : pour pouvoir tirer quelque chose de ces exemples, il serait de bon goût d’avoir quelques connaissances d’un langage de programmation tel que Pascal, C, Lisp ou Java. Il faut dire que j’ai beaucoup d’interlocuteurs qui savent déjà très bien coder, mais n’ont pas le recul nécessaire pour choisir la bonne méthode. Une éventuelle maîtrise de quelques concepts mathématiques est toujours la bienvenue, car je vais évoquer quelques notions qui sont censées faire partie de notre patrimoine scientifique (structure de groupe, relation d’ordre, théorème de la récurrence mais pas beaucoup plus). Ne partez pas ! Il n’y aura rien de très compliqué, c’est promis.

Donc ce livre ne s’adresse pas aux gens allergiques aux sciences ni à ceux qui espèreraient y trouver un manuel de programmation de leur magnétoscope ou de leur four micro-onde. Ouf, j’espère leur avoir fait économiser le prix du livre.

1.3 Que peut-on bien y trouver ?

D’une part, on peut y trouver une panoplie de recettes de cuisine pour résoudre les petits problèmes classiques auxquels nous sommes régulièrement confrontés. Mais ce n’est pas mon but principal. Je voudrais présenter l’algorithmique en suivant les types de problèmes à résoudre plutôt qu’en suivant les structures de données. Trop souvent, les développeurs consacrent une grande quantité de temps au choix de la structure des données avant de réfléchir aux traitements qui s’imposent. Les techniques modernes de développement rapide d’applications conseillent de partir du fonctionnel et d’implémenter la donnée en dernier. J’y reviendrai en détail. Il y aura aussi une grande partie consacrée à l’optimisation des algorithmes. Il s’agit de proposer des stratégies pour améliorer des programmes qui sont inadaptés, algorithme d’une trop grande complexité, programme trop gourmand en temps ou en place mémoire ou même le sentiment vague d’une grande inefficacité (duplication des calculs ou des informations)…

J’ai de nombreuses fois vu des développeurs confirmés choisir une technique ou une autre pour des raisons très éloignées de celles qui devraient nous motiver. Il est bon de connaître un ensemble de techniques permettant de résoudre un problème pour pouvoir, avec le recul du professionnel, choisir la plus adaptée à sa situation ou le meilleur compromis « efficacité/temps de mise au point ». C’est souvent mieux que de prendre la technique la plus élaborée et complexe sous prétexte qu’à ce prix-là, elle doit être bien.

Ce qu’il nous faut, c’est l’idée maîtresse qui se cache derrière les différents algorithmes du même type, et une compréhension plus intime des motivations du programmeur (je ne parle pas que du coût en temps d’exécution).

Je voudrais permettre à mes lecteurs une nouvelle approche, orientée suivant les thèmes profonds de ces algorithmes.

Au sein de chaque grand problème, se trouvent un certain nombre de solutions qui seront ordonnées de la plus simple à concevoir vers la plus efficace, QQCVD^¹¹.

L’essentiel est là : cette synthèse est conçue pour permettre le recul nécessaire au choix d’une stratégie adaptée à un problème. Au delà de ce but simple, je voudrais lui donner les moyens de développer ses propres solutions. Des solutions simples et rapides à développer.

Souvenez-vous que le programmeur travaille toujours en temps limité et que son expérience lui permet rarement de pouvoir estimer correctement le temps de mise au point d’un programme. Bien qu’on ait lu des livres tels que « The mythical man-month »^¹², qui traitent du génie logiciel dans ses grandes longueurs, on se lance encore parfois dans de coûteuses « optimisations » inutiles. J’espère proposer des moyens de bon sens pour permettre le développement d’applications dans le temps imparti et faisant effectivement ce qui est demandé avec une fiabilité suffisante.

N’oublions pas pour autant qu’il y a des durées incompressibles et que l’on ne peut pas créer un bébé en un mois en inséminant 9 femmes. Ce n’est pas en multipliant les développeurs que l’on améliore ou que l’on accélère un développement.

1.4 Comment le lire ?

Evidemment, il est difficile de lire un ouvrage technique de manière linéaire. Une étude de la table des matières permet au programmeur averti, de se ruer sur ce qui est susceptible de l’intéresser, lui faisant peut-être rater du même coup tout l’intérêt de l’ouvrage. J’y ai inclus un index dans l’espoir de permettre une consultation rapide et efficace, mais un glossaire pourrait aussi être utile.

Il y a beaucoup de références croisées et il peut être pénible de les suivre systématiquement, mais dites-vous que c’est seulement le signe du fait que tout se tient. J’ai quelques temps cru que l’informatique était une forêt laissée à l’abandon avec des arbres de toutes tailles poussant de manière désorganisée, mais il suffit d’un pas de côté pour découvrir qu’il s’agit d’un verger où chaque brin a sa place et les branches sont toutes alignées.

1.5 Pourquoi tant de questions ?

L’esprit critique est la base du progrès. Toute évolution part d’une question, ou d’une remise en cause. La question est la base de la plupart des méthodes d’enseignement. Il faut constamment poser des questions. Si possible, les bonnes questions (sic). Ne cherchons pas trop vite la (mauvaise?) réponse dans les livres ou sur Internet !

Faisons mentalement une expérience sadique avec des chimpanzés. Il nous faut en enfermer cinq dans une pièce contenant pour tout meuble un escabeau. Ensuite, nous suspendons une banane au milieu de la pièce en nous assurant que le seul moyen de l’atteindre est d’utiliser l’escabeau. Puis^¹³, nous branchons un système de surveillance qui envoie une douche glacée dans l’ensemble de la pièce dès qu’un chimpanzé monte sur l’escabeau.

Très rapidement, les singes vont apprendre à ne jamais utiliser l’escabeau. Nous pouvons maintenant désactiver le système d’arrosage, il ne servira plus. Remplaçons maintenant un des chimpanzés « dressés » par un nouveau. Le novice va se précipiter vers l’escabeau croyant profiter d’une belle aubaine. La réaction des autres est immédiate. Ne voulant pas être douchés, les quatre autres singes vont lui taper dessus jusqu’à ce que lui aussi comprenne qu’on n’utilise pas cet escabeau.

On peut maintenant remplacer un autre ancien par un autre nouveau. Le même scénario va se reproduire à ceci près que c’est le sixième singe qui tape le plus fort ! Peut-être le sentiment d’injustice ? Continuons à remplacer les singes jusqu’à ce qu’il n’y ait plus aucun des chimpanzés originaux. Nous pouvons ainsi transmettre un savoir de génération en génération. Plus personne ne sait pourquoi, mais on n’utilise pas l’escabeau. C’est une parabole sur la culture d’entreprise, mais aussi sur l’éducation des enfants, sur l’enseignement de manière générale…

Depuis des années, des « mauvais » concepts sont transmis d’une génération à l’autre par le biais de gens qui n’ont pas cet esprit critique. D’autres idées, parfois excellentes, sont prônées par des gens qui ne les appliquent pas ou qui n’en ont pas mesuré les implications^¹⁴. Il faut donc refondre notre savoir et le réorganiser sur des bases rigoureuses. Tout doit être remis en cause.

Il est peut-être possible d’utiliser l’escabeau d’une autre manière, ou même si on se fait la courte échelle. Nous ne saurons pas sans essayer^¹⁵.

2 Formalismes et méthodes

2.1 Conception descendante

2.1.1 Le zen dans l’art du tir à l’arc

Connaissez-vous ces archers extraordinaires qui se concentrent sur une cible toute une journée, parfois même plus longtemps, ensuite ils bandent leurs yeux puis leur arc, et lâchent leur flèche depuis la position du lotus, vaguement dans la direction d’une cible. Le comble, c’est qu’ils l’atteignent...

Evidemment, une flèche par jour, ce n’est pas terrible ! Mais si vous voulez faire de votre travail un art zen, vous pouvez appliquer la méthode. Attention ! Ne trichez pas ! Ne regardez pas le clavier par dessous le bandeau. Si par contre, votre temps est compté, si par malheur vous n’êtes pas un adepte de la méditation transcendantale, il vous faudra déterminer votre cible avant de tirer.

En clair, la réalisation d’un programme part de l’analyse d’un besoin. On cerne un problème avant de tenter de le résoudre. Sinon, il reste toujours la ressource habituelle de tirer d’abord et de nommer la cible ensuite, mais si c’est satisfaisant pour l’esprit, cela ne répond pas au cahier des charges. D’ailleurs, il ne viendrait pas à l’idée d’un ingénieur de lancer ses hommes dans la réalisation d’un travail sans la rédaction préalable d’un cahier des charges. Il s’agit de ne pas répéter un certain nombre d’erreurs historiques telles que la conception de MS-DOS pour les PC ou de VMS. Dans ces deux derniers cas, on est parti d’une machine et on a construit un système en fonction des possibilités techniques plutôt que des besoins de l’utilisateur. Bref, l’utilisateur, à la fin de la chaîne de conception, « n’a qu’à s’adapter ». C’est l’erreur de génie logiciel du XX^ème siècle. C’est une erreur de fond et non une erreur de forme que nous nous efforcerons d’éviter.

Malheureusement, il n’est plus possible, par manque de temps et de compétences, de réaliser de cahier des charges avant de développer. Le concept de time to market est omniprésent. C’est là qu’interviennent les techniques d’« Extreme Programming » que nous développerons plus tard au chapitre 7.

2.1.2 Des pyramides et des arbres

Comment éviter ce type d’erreur ? Déjà, il faut avoir une vision claire du développement d’applications. La plupart des programmeurs ont tendance à voir leurs œuvres comme une belle pyramide. Chaque pierre de la structure a été conçue amoureusement puis assemblée indépendamment du fait qu’elle soit utile ou non. Lorsqu’on leur demande à quoi sert telle ou telle partie, la réponse est souvent : « Ah non! Ça ne sert pas, mais je croyais que ce serait utile » ou bien « Tiens ! C’est encore là ! » et même des « Mais ça va bientôt servir, enfin je crois... » et j’en passe. Quand l’expérience a fait son travail, le programmeur voit son programme comme un arbre. Un arbre dont la racine est le coordonnateur des procédures les plus globales (en général, c’est l’interface graphique qui permet le mieux de réaliser ce travail de coordination) et dont les feuilles sont les unités les plus simples. Comme pour l’arbre, son travail pousse depuis la racine vers les feuilles. La structure finale est équivalente. C’est le sens de la croissance qui est inversé. Le résultat est, par construction, adapté au besoin. De même, nos programmes seront corrects par construction. Depuis la conception jusqu’à la réalisation finale, nous nous attacherons à garder cette structure. Attention, il existe de mauvais arbres et de bonnes pyramides. Mais, il ne faut pas céder systématiquement à la tendance naturelle à développer en ascendant.

Pour être plus clair, j’imagine qu’un problème peut être attaqué depuis le côté fonctionnel (typiquement par l’interface graphique) mais que simultanément, ayant une bonne idée des traitements nécessaires sur l’ensemble des données, j’ai une autre équipe qui s’occupe d’un module de plus bas niveau, comme l’accès à une base de données. Je suis certain que ce module va servir. On peut imaginer beaucoup de changements d’ordre structurel, mais l’architecture de cette application contiendra toujours une base de données, ou alors je suis vraiment un mauvais architecte logiciel. Ce module est à la base de la pyramide et donc correspond à une partie ascendante. L’interface et ces dépendances sont à la racine de l’arbre correspondant à la conception descendante.

Bref, les conceptions ascendante et descendante peuvent être compatibles pour peu que le coordinateur du projet ait les idées claires.

2.1.3 Le développement champignon

C’est l’autre défaut de base qui s’ensuit : le programme au stade embryonnaire se met a grandir par petites excroissances, pas forcément adaptées les unes aux autres. Très rapidement, l’ensemble devient entièrement illisible. Ayant produit un programme « pas encore complètement au point » (traduisez « désespérément irrécupérable »), le programmeur se met alors dans une phase dite de « déboguage ». C’est une période très particulière, qui peut prendre quatre à dix fois plus de temps que le temps de développement du produit correct, pendant laquelle le programmeur est de très mauvaise humeur.

Ce qui s’explique : il va devoir, par petits « coups de tournevis » successifs, tenter de transformer son œuvre pour la faire correspondre à ce qui était demandé. Chacun d’entre nous est passé par là et je ne suis pas le premier à jeter la pierre^¹⁶. Chaque petit champignon de programme se met à pousser un peu partout. Le résultat est une sorte de structure à excroissances multiples dont l’organisation ne peut être expliquée ni comprise, même par son concepteur. La moindre modification devient un cauchemar pour le développeur. Il est impossible d’en prévoir les répercussions. D’autre part, il y a en général d’autres facteurs qui interviennent : les délais étant dépassés, plusieurs membres de l’équipe sont licenciés ou mutés vers d’autres tâches, on fait venir des spécialistes qui n’y comprennent forcément pas grand-chose non plus. Le projet peut ainsi mourir de sa belle mort avec en conclusion, une grande fête où l’on récompense les non participants.

Et lorsque le programme a pris une ampleur suffisante, le programmeur découvre des erreurs de conception. Mais il considère qu’il est trop tard pour recommencer. Plus le temps lui manque, et plus il est persuadé qu’il lui faudrait plus de temps pour réécrire un programme correct que pour corriger le travail déjà réalisé. Pourtant, la moindre modification de fond l’oblige à des centaines de corrections dont certaines lui échappent.

En fait, il faut reprendre à la phase de conception ! Il est infiniment plus rentable de programmer les modules à la demande. Décrire parfaitement des scénarii^¹⁷ d’utilisation avant de proposer une quelconque réponse. Car lorsqu’un programme fonctionne mal, en général, c’est la conception qui est en cause, plus que l’expression, et il est alors difficile de revenir sur ses choix de départ. La structure du programme doit être apparente du début du projet à sa fin. Si la structure employée au départ se révèle inadaptée, il faut concevoir à nouveau sur des bases saines.

2.1.4 La programmation à la demande

Poussons notre idée jusqu’au bout : tout projet démarre avec, au moins, un vague cahier des charges fonctionnel. Aujourd’hui, on y met des scénarios d’utilisation du logiciel. Les meilleurs systèmes sont conçus à partir du manuel de l’utilisateur. Ainsi les fonctionnalités sont celles dont on a besoin et non celles que l’on croit pouvoir implanter facilement. On peut aussi commencer par construire l’interface utilisateur pour bien identifier toutes les utilisations possibles. L’idéal serait de programmer depuis le programme principal vers la plus petite unité. La méthode ultime demanderait d’écrire les fonctions depuis les plus globales vers celles du plus bas niveau^¹⁸. On ne définirait une fonction que lorsqu’elle aurait été appelée.

Il s’agit de programmer à la demande afin d’éviter le code mort.

2.1.5 Revenons sur terre

Cela demande une grande discipline. Malheureusement, dans un langage de type Pascal où chaque objet doit être défini avant d’être utilisé, cela veut dire que l’on doit écrire le programme de la fin vers le début. Et alors on ne pourrait tester le programme qu’après l’avoir entièrement écrit. Ce n’est pas praticable. En Lisp, c’est possible parce que l’évaluation est elle-même faite à la demande et qu’il n’y a pas de phase de compilation. En Java, grâce aux interfaces, il est possible de faire quelque chose d’approchant.

Chaque module sera entièrement spécifié par une classe de type interface, qui ne correspond à aucun code exécutable, mais qui permettra de construire la classe appelante de manière indépendante de l’implémentation. On peut alors faire une implémentation préliminaire du module qui ne fait qu’afficher un message « non implémenté » à chaque utilisation des fonctionnalités du module. Il sera possible, au fur et à mesure du développement, de remplacer les fausses classes par les vraies. Ce qui est certain, c’est que le cadre du développement est déjà fixé et que personne n’est bloqué par l’attente d’un module : il est véritablement possible de faire le développement en parallèle de deux modules dépendants. On peut même les tester indépendamment.

De manière générale, nous nous bornerons à la conception descendante et pour la programmation effective, nous aurons recours à des méthode mixtes, mêlant alternativement phases ascendantes et descendantes. Il nous faudra passer par quelques essais pour trouver le bon compromis. Par contre, pour les phases de réécriture, je reste résolument en faveur de solutions entièrement descendantes.

La phase de conception est déterminante pour tout le projet. Il est possible d’améliorer sensiblement la qualité de ce travail par la rédaction anticipée du rapport final. Cet effort de rédaction permet de reconsidérer les choix d’implantation à la lumière de l’expérience. Le simple fait d’essayer d’expliquer ses choix permet de les remettre intelligemment en cause.

Il est même indispensable de rédiger une première version du manuel de l’utilisateur avant d’avoir commencé à programmer. Il est contraignant de la maintenir à jour, mais c’est un prix à payer pour maintenir les idées claires pour tous.

Avec les nouvelles techniques de développement d’applications, la phase de conception n’est close qu’à la recette finale. Il faut donc bouleverser la chronologie classique du développement.

Donnez-vous le droit d’écrire le manuel de l’utilisateur, puis de programmer l’interface avec l’utilisateur puis de prendre les décisions finales sur la structure de la base de données. Si vous commencez par la base de données, lors de la dernière phase, il est certain que vous devrez changer la structure des tables, modifier des noms de champs, transformer des vues en table ou pire. Résultat, il faudra repasser par la phase de codage.

Cent fois sur le métier remettez votre ouvrage… N’ayez pas peur de réaliser plusieurs prototypes et de reprendre plusieurs fois à la phase de conception. Une fois que l’on a admis qu’il n’y a pas de réponse universelle, on accepte plus facilement de consacrer du temps à améliorer ses méthodes de travail et celles de son équipe.

2.2 Type de données abstrait

Nous allons donc proposer un formalisme permettant de préciser la structure et les propriétés des informations que nous manipulons dans nos programmes. Ne nous laissons pas tromper par le titre, les types abstraits sont en fait très concrets dans la pratique. Ils forment en même temps la base du paradigme objet.

2.2.1 Le plus rigoureux possible ?

Commençons par des exemples simples. Progressivement, cela deviendra complexe sans devenir compliqué, je l’espère. Il n’est pas question de pousser le formalisme autant que Marie-Claude Gaudel, Michèle Soria et Christine Froidevaux dans le livre « Types de données et algorithmes ». C’est tellement compliqué qu’il n’y a aucun moyen de relier l’exposé à la pratique^¹⁹. Alfred Aho, Jerry Hopcroft et Jeffrey Ullman sont beaucoup plus concrets dans leur livre « Data structures and Algorithms »^²⁰.

Nous ne pousserons pas le modèle au-delà de ses limites. Nous l’utiliserons tant qu’il nous aidera à comprendre. Dès que cela devient lourd, il faut s’arrêter.

Voici la structure initiale :

Sorte : nom du type abstrait

Utilise : les types abstraits sous-jacents

Opérations : le profil des différentes fonctions et constantes à implémenter

Préconditions : la description du domaine de définition de ces fonctions

Axiomes : l’ensemble des propriétés naturelles et intrinsèques de ces fonctions et constantes

Type abstrait 2.2.1.1 le formalisme de base

Ceci représente la signature du type. Quelques exemples ne seront pas de trop.

Tant que nous en restons là, les objets gardent une pureté quasi mathématique et le terme « fonction » correspond parfaitement à celui des maths. Plus tard, lors de la programmation effective, ils risquent de perdre cette pureté.

2.2.1.1 Les entiers naturels

Avec ceci, il est facile de construire notre propre version des entiers naturels et surtout de bien en cerner les propriétés. Il nous faut une relation d’ordre (est-un-prédécesseur-de) et la propriété fondamentale des entiers naturels, à savoir :

Toute partie non vide de l’ensemble des entiers naturels admet un plus petit élément.

Ca y est, nous avons le théorème de la récurrence (cf. 3.2.1.1).

Sorte : Entier

Utilise : Booléen

Opérations :

Zéro : ® Entier (c’est une constante)
Successeur : Entier ® Entier
Nul? : Entier ® Booléen

Préconditions : aucune !

Axiomes :

" n Î Entier, non Nul?(n) Þ $ n’ / n=Successeur(n)
" n, n’ Î Entier, Successeur(n)=Successeur(n’) Û n=n’

Type abstrait 2.2.1.2 les entiers naturels

Voilà ! C’est très simple et on arrivera à en tirer quelque chose d’utile par la suite.

2.2.1.2 Les entiers naturels munis de + et de –

Pour étoffer notre premier exemple de type abstrait simpliste, rajoutons-lui l’addition et la soustraction.

Opérations :

+ : Entier , Entier ® Entier
– : Entier , Entier ® Entier
≤ : Entier , Entier ® Booléen

Préconditions :

a – b n’existe que si a ≥ b

Axiomes :

" a Î Entier, a + Zéro = a
" a Î Entier, a – Zéro = a
" a,b Î Entier, a + b = b + a
" a,b Î Entier, Successeur(a + b) = Successeur(a) + b
" a,b Î Entier / a ≥ b, Successeur(a) – Successeur(b) = a – b

Type abstrait 2.2.1.3 entiers naturels, +, –

Ces quelques axiomes suffisent à décrire complètement les opérations en question. Prolog n’en demande pas plus pour vous permettre des opérations sur les entiers ainsi définis. C’est en général le premier exemple qu’on propose en Prolog.

2.2.1.3 Les listes dans la version la plus simple

Passons maintenant à un exemple plus pratique pour lequel nous ferons la traduction vers un langage de programmation.

Sorte : Liste

Utilise : (Elément, =), Booléen

Opérations :

Liste_vide : ® Liste
Cons_liste : Elément , Liste ® Liste
Tête : Liste ® Elément
Suite : Liste ® Liste
Vide? : Liste ® Booléen

Préconditions :

Suite(l) n’existe que si non Vide?(l)
Tête(l) n’existe que si non Vide?(l)

Axiomes :

" l Î Liste, " e Î Elément, Suite(Cons_liste(e,l))=l
" l Î Liste, " e Î Elément, Tête(Cons_liste(e,l))=e

Type abstrait 2.2.1.4 les listes récursives

Nous venons ainsi de définir une interface universelle avec les objets de type Liste. Nous pouvons ensuite implémenter les listes avec des cellules chaînées ou avec des tableaux voire même des fichiers (Je l’ai déjà vu faire de manière très lisible). Tous les algorithmes que nous aurons conçus pour les listes pourront ainsi fonctionner sans réécriture.

Tout ce que nous allons construire par la suite sur ce type sera toujours valable. Nous avons l’équivalent d’une interface de Java qui nous permettra véritablement d’appliquer la stratégie descendante ou de lancer en parallèle le développement des traitements des listes et le développement de leur implémentation.

Cela ressemble beaucoup à la définition des entiers. Nous pouvons ensuite définir les opérations telles que longueur, concaténation et bien d’autres.

2.2.1.4 Des listes aux piles et aux files

On peut aisément concevoir la programmation d’un type file d’attente et d’un type pile, basée sur nos listes sans avoir encore décidé ni du langage, ni de la structure physique de nos listes.

2.2.1.4.1 LIFO

Voici d’abord les listes LIFO (« last in first out ») qui sont appelées communément piles. On traite les éléments dans l’ordre inverse de leur arrivée.

Sorte : LIFO

Utilise : (Elément, =), Booléen

Opérations :

pile_vide : ® LIFO
empile : Elément , LIFO ® LIFO
sommet : LIFO ® Elément
dépile : LIFO ® LIFO
vide? : LIFO ® Booléen

Préconditions :

dépile(p) n’existe que si non vide?(p)
sommet(p) n’existe que si non vide?(p)

Axiomes :

" p Î LIFO, " e Î Elément, dépile(empile(e,p))=p
" p Î LIFO, " e Î Elément, sommet(empile(e,p))=e

Type abstrait 2.2.1.5 les piles (LIFO)

C’est un ordre assez naturel quoique l’on pense. Il correspond à de nombreux schémas de fonctionnement, comme celui de l’homme qui pense à un idée, est interrompu par un coup de téléphone, puis reprend le cours initial de sa pensée. C’est aussi le fonctionnement de la plupart des interprètes qui évaluent une expression en empilant toutes ses sous expressions.

Il est d’autre part évident qu’il s’agit d’une transposition du type Liste de tout à l’heure. Il suffit de renommer

tête ® sommet

suite ® dépile

cons ® empile

liste_vide ® pile_vide

vide? ® vide?

2.2.1.4.2 FIFO

Et voici les files d’attentes : les listes FIFO (« first in first out »), la version équitable pour les usagers qui attendent^²¹. On gère les éléments dans leur ordre d’arrivée comme aux caisses du super marché^²².

Sorte : FIFO

Utilise : (Element, =), Booléen

Opérations :

pile_vide : ® FIFO
empile : Elément , FIFO ® FIFO
sommet : FIFO ® Elément
dépile : FIFO ® FIFO
vide? : FIFO ® Booléen

Préconditions :

dépile(f) n’existe que si non vide?(f)
sommet(f) n’existe que si non vide?(f)

Axiomes :

Et là patatras ! Le formalisme est ici impuissant à décrire de manière simple le fonctionnement de la pile. C’est facile à expliquer, mais il faut décrire d’autres opérations comme dernier_élément ou longueur pour pouvoir exprimer les propriétés intrinsèques des files.

Type abstrait 2.2.1.6 les files d’attente (FIFO)

D’une part, il n’est pas nécessaire de décrire ces propriétés pour pouvoir les programmer efficacement.

D’autre part, ces propriétés ne nous apportent rien du point de vue programmation.

Pour combler le vide des axiomes du type abstrait, nous allons recourir aux exemples : Exemple 2.2.1.1 et Exemple 2.2.1.2. Les programmes sont plus explicites que des expressions mathématiques inadaptées.

function empile(e:element;f:file):file;
begin
  if vide(f) then
    return(cons(e,f))
  else
    return(cons(tete(f),
                empile(e,suite(f))))
end;

pile_vide ¬ liste_vide
sommet ¬ tête
depile ¬ suite
vide ¬ vide?

Exemple 2.2.1.1 file d’attente avec insertion en fin (Pascal)

function depile(f:file):file;
begin
  if vide(suite(f)) then
    return(pile_vide)
  else
    return(cons(tete(f),
                depile(suite(f))))
end;
function sommet(f:file):element;
begin
  if vide(suite(f)) then
    return(tete(f))
  else
    return(sommet(suite(f)))
end;

pile_vide ¬ liste_vide
empile ¬ cons
vide ¬ vide?

Exemple 2.2.1.2 file d’attente avec insertion au début (Pascal)

Telles que nous les avons définies ici, les files d’attentes sont très inefficaces et demandent un traitement soit à l’entrée dans la file d’attente (le premier exemple), soit à la sortie (le deuxième). Mais je suis sûr qu’elles fonctionnent. Il sera toujours temps après de les représenter comme dans l’exemple en C qui suit. Il est quand même nécessaire d’avoir un ordre d’idée de la taille maximale nécessaire car nous allons utiliser un tableau d’éléments.

t_element tableau[Taille_max];
int indice_sommet=0;
int indice_fin=0;
void empile(t_element element) {
  tableau[indice_sommet]=element;
  indice_sommet=(indice_sommet+1)%Taille_max;
}
t_element sommet() {
  /* eventuellement vérifier que
        indice_fin !=indice_début */
  return tableau[indice_fin];
}
void depile() {
  /* eventuellement vérifier que
        indice_fin !=indice_début */
  indice_fin=(indice_fin+1)%Taille_max;
}

Exemple 2.2.1.3 file d’attentes en tableau (C)

C’est une version impérative. Il n’y a qu’une seule file d’attente (variable globale) et nous nous sommes passablement écartés du type abstrait.

Notez bien que s’il fallait en faire quelque chose de professionnel, il y aurait beaucoup de choses à ajouter comme des vérifications sur la taille aussi bien au remplissage qu’à la vidange. L’objectif n’était pas d’écrire un programme, mais de montrer comment l’expression évolue pendant le passage du type abstrait au programme final.

2.2.2 Un peu de souplesse !

Il n’est donc pas question d’épuiser notre temps et notre patience à créer des types abstraits pour la beauté du geste. Cela peut vite devenir trop gros ou trop compliqué. Mieux vaut découper en plusieurs types abstraits faciles à cerner que nous composerons plus tard.

Quant aux axiomes, nous ne les exprimerons que lorsqu’ils nous semblent utiles. En effet, ils ne suffisent pas toujours à décrire les propriétés caractéristiques des données de manière suffisamment précise pour que l’on puisse les programmer en direct. D’autre part, les propriétés caractéristiques ne sont pas toujours apparentes immédiatement.

Conclusion, nous travaillerons avec des versions simplifiées des types abstraits et nous laisserons de côté les formalismes lorsqu’ils n’auront plus rien à nous apporter. C’est un bon principe que l’on retrouve en physique : nous pratiquons gaiement la physique de Newton dans les limites où elle modélise bien le monde qui nous entoure, mais dès que nous flirtons avec la vitesse de la lumière^²³, nous passons à la physique quantique et aux formules de Lorentz. Bref, n’utilisons pas un modèle en dehors de ses limites.

2.2.3 En langage naturel !

Nous allons programmer l’algorithme de tri par insertion en langage naturel pour un joueur de cartes.

La main droite contiendra le jeu trié (la Sorte que nous voulons définir)

La main gauche contient les cartes distribuées en vrac au départ (le type Liste qu’on Utilise)

Le joueur va insérer à sa place chacune des cartes de sa main gauche dans sa main droite (l’Opération que l’on va définir qui prend une main de cartes en vrac et qui rend une main de cartes triées)

Type abstrait 2.2.3.1 mains triées

Avec cette description très informelle du tri, nous allons pouvoir démontrer de manière rigoureuse^²⁴ que le programme aboutit correctement avec une main droite triée.

Hypothèse de départ, la main droite est vide. Donc elle est triée.
Hypothèse de récurrence, si on insère à la bonne place une carte dans une main triée, celle-ci conserve cette propriété.
En vertu du théorème de la récurrence^²⁵, la main droite est toujours triée. Comme de plus, la main gauche contient un nombre fini de cartes au départ et que chaque étape en fait passer une de la main gauche à la main droite, le programme termine en autant d’étapes qu’il y avait de cartes au départ dans la main.

Nous n’avons pas détaillé l’algorithme d’insertion de la carte à la bonne place. C’est volontaire dans la limite où la programmation de cette opération ne pourra jamais rendre compte de la complexité de ce qui se passe dans l’esprit d’un être humain. En effet, nous embrassons d’un seul coup d’œil l’ensemble de la main et nous avons de plus le souvenir des cartes qui y figurent. Nous savons déjà approximativement où la carte doit aller. En conséquence, nous sommes plus efficace dans notre insertion qu’un simple parcours linéaire ou même qu’une dichotomie. Selon la structure informatique choisie et les particularités des objets à trier, diverses optimisations algorithmiques nous seront accessibles.

2.2.4 Jusqu’où doit-on aller ?

On peut composer et empiler des dizaines de types abstraits pour arriver à décrire complètement un problème. Pour économiser le temps du passage à la programmation, il me semble judicieux d’utiliser le langage UML pour modéliser des classes plutôt que des types abstraits avec un logiciel qui permet de générer automatiquement le code^²⁶. Mais UML ne décrit que les rubriques Sorte, Utilise et Opérations du type abstrait et il ne faut pas oublier par la suite de rajouter des commentaires au code généré pour exprimer les rubriques Préconditions et Axiomes.

Mais comme tout formalisme, les types abstraits ont non seulement des limites, mais ils peuvent s’avérer d’un emploi excessivement lourd. Il faut donc chercher des compromis. Tout au long de cet ouvrage, nous tenterons de garder la philosophie des types abstraits en proposant un code réaliste et simple pour trouver un bon compromis entre la rigueur et la convivialité.

Nous garderons toujours le souci de la lisibilité et de la simplicité sans sacrifier l’essence et l’intégrité du concept.

Pour ceux qui connaissent les grammaires attribuées^²⁷, il en est de même : c’est l’esprit et la méthode programmation qui prime. S’il est plus pratique de laisser de côté le paradigme un instant pour développer une partie spécifique, nous n’hésiterons pas une seconde. D’autre part, il n’est pas nécessaire d’avoir un logiciel d’évaluation des grammaires attribuées pour bénéficier de leur puissance d’expression. Il y a des attributs synthétisés qui représentent l’information qui remonte vers la racine de l’arbre et les attributs hérités qui sont l’information descendante. On peut implémenter les visites des nœuds avec des fonctions de parcours d’arbres dont les paramètres seront les attributs hérités et le résultat les attributs synthétisés.

Je demande pardon à tous ceux que ce dernier paragraphe a dérouté. Je ne recommencerai plus, c’est promis.

Pour ce qui est de l’état d’esprit et la méthodologie qui priment sur l’expression et la forme, on peut illustrer avec l’exemple du langage ADA qui fut créé avec l’espoir d’imposer l’esprit avec la forme. C’est un échec aux proportions planétaires : un habitué du Fortran reconverti de force à ADA peut continuer à écrire du Fortran à peu de choses près et toutes les contraintes syntaxiques peuvent être contournées à grand renfort de sucre syntaxique. On peut ainsi construire des programmes très longs et parfaitement abscons.

La constatation est simple, les contraintes du langage diminuent le pouvoir d’expression mais pas la capacité à faire des bêtises. La discipline doit venir d’ailleurs. Il vaut probablement mieux réunir l’ensemble de l’équipe de développement pour leur faire prendre une part active à l’organisation et aux travaux de normalisation du développement (nomenclature etc.).

3 Programmation

3.1 Introduction

3.1.1 Clarté ou efficacité

Deux concepts souvent antinomiques. Tout est dans l’art de trouver des compromis. Il nous faut programmer des applications qui aboutissent à des résultats en un temps raisonnable (qui soient « efficaces » en terme de temps d’exécution), sans toutefois y sacrifier un temps de développement trop important, tout en gardant à l’esprit la lisibilité et la compréhensibilité du code pour la maintenance (beaucoup de choses pour un seul homme !). La vie du programmeur est bien compliquée ! Mais il doit saisir rapidement que le plus important est dans la clarté du développement. Optimiser est un jeu d’enfant sur un programme conçu avec simplicité, si l’on garde toutefois la version simple originale en commentaire. De même, communiquer avec ses collègues (et tout son entourage) est difficile bien que primordial et nécessite un langage simple et lisible. Les machines sont de plus en plus puissantes. Le temps de l’ingénieur est de plus en plus coûteux. Les gens sont de plus en plus nombreux sur le même projet. Autant de raisons de privilégier la lisibilité au détriment d’une soi-disant efficacité d’exécution ! Il n’y a d’efficacité réelle que dans la clarté !

Nous allons aborder quelques détails permettant d’améliorer cette clarté, entre autres, une petite section est consacrée aux normes d’indentation et de nomenclature. Vous noterez que je propose plusieurs « vérités universelles ». Je ne suis pas un ayatollah de telle ou telle méthode, mais je conseille vivement que les partenaires d’un même projet se mettent d’accord pour entériner un style fixé pour l’indentation et pour la nomenclature des modules, des classes et des variables.

3.1.1.1 Y a-t-il un langage universel dans la salle ?

Le langage utilisé presque partout pour l’enseignement de base de l’informatique est le Pascal. Lors de sa conception, la théorie des langages en était à ses balbutiements. N. Wirth a conçu son langage à des fins didactiques en gardant à l’esprit toutes les corrections nécessaires à apporter aux langages de l’époque (Fortran, Cobol...). Aujourd’hui encore, malgré les problèmes induits directement par la syntaxe du langage, on se rend compte du gouffre théorique qui avait été comblé à l’époque. Attention, le Pascal n’est en aucun cas un langage dédié à l’écriture d’application. Il n’est utile que pour le prototypage et pour décrire nos structures et nos algorithmes. Maintenant, la science a quand même bien progressé et le Pascal qui, hier semblait être la solution universelle, semble aujourd’hui complètement inadapté à l’enseignement et encore plus au développement d’applications. Je dis bien « semble ». D’autres langages, tels que Ml, Scheme etc., ont leurs défenseurs, mais s’ils sont excellents pour décrire nos problèmes, ils ne sont pas assez connus du commun des programmeurs^²⁸. Pourtant, il nous faut bien passer par un langage commun. Nous allons tenter de nous affranchir de l’unicité du langage pour dégager ce qui peut être exprimé indépendamment.

3.1.1.2 Langages utilisés

En fait, il existe plusieurs paradigmes de programmation plus ou moins incompatibles et nous verrons autant que possible des exemples dans chacun d’entre eux :

La philosophie impérative est la moins populaire, la plus ancienne, mais elle reste très pertinente. Elle sera représentée par Pascal et par C. Je n’ai aucun exemple à présenter en assembleur ou en langage machine. Sachez quand même que Donald Knuth donnait tous ces exemples en Fortran dans son premier tome. Cela ne nuisait pas à la compréhension.

La philosophie fonctionnelle est représentée ici par Lelisp de l’INRIA. J’aurais pu choisir ML ou même CaML qui sont très pédagogiques, ou même choisir un autre dialecte de Lisp comme Scheme ou CommonLisp. Mais j’aime bien Lelisp et je l’ai beaucoup pratiqué.

En ce qui concerne le paradigme objet, j’ai choisi Java qui reste mon langage préféré. Je l’ai préféré à d’autres langages objets comme Smalltalk ou Simula moins en vogue et aux langages « orientés » objet comme C++ (et Ada qui prétend être orienté objet, mais qui traîne tous les défauts de l’impératif alliés à une lourdeur syntaxique phénoménale).

Il y a aussi la programmation logique et son unique représentant : le Prolog. A part deux ou trois algorithmes dont l’implémentation en Prolog présente un grand intérêt par sa concision, il ne me semble pas intéressant de présenter d’exemples en Prolog.

3.1.1.2.1 Lisp (lelisp de l’INRIA)

L’intérêt de présenter des exemples de programmations dans ce langage est sa simplicité d’expression et sa concision. De plus, ne confondant pas l’idée avec les mots qui l’expriment, nous chercherons à trouver l’expression qui s’en rapproche le plus (la plus simple, QQCVD). Il s’agit de décrire les solutions et de laisser travailler la machine. Le dialecte de Lisp utilisé présente les fonctions de bases suivantes :

defvar : pour la définition de variables et setq pour la modification de leur valeur.

de : pour la définition de fonctions évaluant leurs arguments: (lambda)

df : pour la définition de fonctions n’évaluant pas leurs arguments : (flambda)

dmd : pour la définition de macro-fonctions^²⁹ : (mlambda)

Pour ceux qui n’en ont jamais écrit, je vais expliquer rapidement comment le lire. Toute expression Lisp est, soit un atome (symbole, nombre ou chaîne), soit une liste d’expressions entre parenthèses. Toutes les expressions ont une valeur. Par contre, le typage est (très) faible : une fonction prend des arguments de type quelconque tant que c’est possible (par exemple, une soustraction prendra quand même des arguments numériques). L’évaluation d’une expression Lisp de type liste, est obtenue en appliquant la fonction (le premier élément de la liste) à ses arguments (les autres éléments de la liste). Par exemple, (* 2 3 4) sera évalué à 24. Autre exemple, la fonction if, l’expression

(if (< a b)
b
a)

rendra le plus grand parmi a et b^³⁰. Cette fonction n’évalue que les expressions nécessaires : l’évaluation de

(if (print (< 1 2))
(print 1)
(print 2))

rendra 1, mais produira l’effet de bord d’imprimer les valeurs t et 1, mais pas 2.

3.1.1.2.2 Pascal et C

Dans ces langages, il faut tout faire « à la main », y compris réserver et libérer la place mémoire... Mais leurs possibilités sont immenses, pour peu que l’on soit discipliné. La traduction de l’un dans l’autre ne devrait poser aucun problème. Nous montrerons des exemples côte à côte pour nous en persuader. Le Pascal décrit dans nos exemples aura quand même quelques particularités :

return sera introduit pour rendre les résultats des fonctions. Nous éviterons d’en utiliser l’effet de bord qui arrête l’évaluation^³¹.

or et and seront considérés comme séquentiels de gauche à droite et n’évaluant que ce qui est nécessaire^³².

En ce qui concerne le langage C, afin de comprendre à la fois sa puissance et ses limites, rappelons que lors de sa conception, on voulait un langage pour créer un système d’exploitation et des compilateurs de tous les autres langages pour leur permettre de fonctionner dans cet environnement. On ne peut pas penser au C, sans voir les objectifs d’UNIX et MULTIX.

Le langage est conçu pour permettre la gestion de la pile d’évaluation pour implémenter le multitâche et pour gérer les moindres détails de fonctionnement de toutes les machines possibles.

En conséquence, c’est un langage de développeur, extrêmement puissant et souple. En contrepartie, si tout est possible pour le programmeur expérimenté, il n’y a pas de garde-fou pour protéger le commun des mortels. Bien qu’il soit très puissant, c’est un langage de très bas niveau (proche de la machine) et on ne peut pas, par exemple, créer des fonctions dans un environnement local. Considérez le C comme un gigantesque assembleur.

3.1.1.2.3 Java

C’est un langage relativement récent, dans lequel j’ai trouvé toutes les caractéristiques que j’espérais trouver dans le C++. Il y a d’abord le typage fort et le polymorphisme qui s’intègre si bien à la philosophie objet. Les règles de visibilité de l’information sont extrêmement claires et grâce aux variables de classe, on peut vraiment créer des données qui ne sont visibles que là où elles sont pertinentes^³³.

Parmi les fonctionnalités qui en font un très bon langage pour le développement rapide de prototypes, il y a :

La gestion automatique de la mémoire, c’est-à-dire le « garbage collector ». Le système se charge d’allouer et de libérer la mémoire au besoin.

Les interfaces, c’est-à-dire ces fameuses classes qui permettent de décrire les points de liaison entre les modules.

Les javadocs, qui sont en l’occurrence, le moyen royal de documentation du code : on commente les classes, les méthodes et les variables à leur création et le système génère un document hypertexte qui permet de comprendre et d’utiliser ces classes.

L’existence d’un grand nombre de bibliothèques de structures et de méthodes gérant ces structures qui rendent bien des parties de cet ouvrage obsolètes : il existe des tables de hachages, des listes, des vecteurs et une foule d’autres structures moins basiques, munies de toutes les méthodes nécessaires.

3.1.1.3 Nomenclature

Afin de pouvoir se comprendre entre programmeurs, il est nécessaire d’avoir des normes de nomenclature des objets, fonctions, variables, modules etc. et des normes d’indentation rigoureuses. Il existe peut-être autant de normes que de programmeurs et les miennes ne sont pas forcément les meilleurs. Par contre, je vais les suivre de manière systématique. Il se trouve que l’habitude veut que les normes usuelles de nomenclature ne soient pas du tout les mêmes pour les langages que je vais utiliser. Je vais donc les décrire succinctement :

Pour tous les langages que j’utilise, je préfère les noms de variables explicites aux acronymes et abréviations ambiguës sauf pour les variables représentant des objets trop courants dans un programme :
- Les entiers :
  - i, j et k pour les indices de tableaux
  - n, m pour les entiers naturels
- Les flottants :
  - x, y et z pour représenter des réels
  - x0, x1, x2 et y0 etc. pour des coordonnées
- Les listes dans des programmes génériques de traitement de liste : l ou l1, l2 etc.
Pour C, lelisp et Pascal :
- Les noms de variables sont composés de mots séparés par un souligné « _ ». par exemple : liste_des_nombres_premiers_calcules
- Les noms de types sont préfixés de ‘t_’par exemple : t_date
Pour Java :
- les noms de variables composés sont construits en séparant les mots par mise en majuscules de la première lettre de chaque mot à partir du deuxième^³⁴ : listeDesNombresPremiersCalcules
- Il en est de même pour les noms de méthodes et de modules (package) qui ne peuvent être confondus avec les noms de variables de par leur place dans la syntaxe de Java.
- Les noms de classes (équivalent des types en C et Pascal) sont différentiés par une majuscule au début : Date

3.1.1.4 Indentation

Pour ne pas avoir un style trop différent dans chacun des langages utilisés, j’applique une règle systématique pour les instructions : à chaque descente d’un niveau de profondeur dans les instructions, je rajoute un paire d’espaces à l’indentation. C’est valable dans tous les langages. Si je dois regrouper des instructions dans un bloc (entre accolades pour C et Java, begin et end en Pascal), je les décale d’un niveau de plus sauf les accolades des expressions if ou while et pour les fonctions où j’utilise la forme :

if (expression_booleenne(args)) {
instruction_de_niveau2(arg1,arg2);
} else {
autre_instruction_de_niveau2;
}

Ne vous inquiétez pas, vous vous habituerez.

Pour les expressions trop longues, l’habitude est de mettre en colonne les sous éléments du niveau suivant :

fonction_longue(long1+long2+long3+long4)

peut être réécrit comme ceci :

fonction_longue(long1+
                long2+
                long3+
                long4)

De la même manière si le séparateur n’est pas un "+" mais une virgule, les virgules restent en fin de ligne.

Pour les exemples en Lelisp, c’est la règle des expressions trop longues qui servira, du fait qu’il n’y a que des expressions en lisp et pas d’instructions.

(fonction_longue arg1 arg2 arg3)

se réécrira comme ceci :

(fonction_longue arg1
arg2
arg3)

3.1.2 Prototypage

Pour évaluer le coût de développement d’une idée, il faut déjà en implémenter une version simple. Ne serait-ce que pour vérifier sa complexité dans la pratique et valider son expression. Un petit effort est nécessaire en matière d’interface utilisateur. Non pour des raisons commerciales, mais pour permettre de tester correctement. Il faut en fait réaliser une succession de prototypes et éviter autant que possible de réutiliser le code de la version n pour la version n+1. Chaque prototype devra être écrit d’un seul morceau, afin d’en assurer la cohérence. C’est douloureux de jeter du code mais c’est nécessaire à la progression. Chaque version sera à la fois plus puissante et plus simple.

Recommencer à zéro permet d’améliorer les choix de bases. A la fin, le produit doit être parfaitement lisible, pour permettre à d’éventuels correcteurs de travailler efficacement, et parfaitement au point pour permettre de l’utiliser comme une boîte noire. Il faut gérer les différentes versions. Il existe des systèmes de gestion des versions des différents modules, sous UNIX par exemple, il existe SCCS, RCS et CVS qui a été porté sous Windows sous le nom WinCVS. Nous en parlerons au chapitre 7.5.

Pour faire de bons composants « utilisables », dites-vous que beaucoup de gens font des composants « réutilisables » mais que personnes n’en utilise. Le prototype permet de valider cette utilité. Nous verrons comment s’implique l’utilisateur dans cette validation pendant tout le chapitre 7.

3.1.3 Le coût de la mise au point

Evaluer le prix et la durée d’un développement est un travail très difficile qui demande une grande expérience de la conduite de projet de la programmation. Comme il dépend aussi de la qualité de l’équipe et des outils utilisés, je ne peux que proposer une aide qualitative pour maintenir ce coût dans des limites acceptables.

3.1.3.1 Au niveau stratégique

Dans un domaine encore aussi mal connu que l’informatique, peu de gens sont capables de déterminer le coût de mise au point d’un logiciel dans une fourchette raisonnable. Le coût est essentiellement fonction du temps passé multiplié par le nombre de programmeurs auquel s’ajoute le prix du matériel et des logiciels. En fait, cela dépend aussi énormément du nombre de personnes que l’on aura à coordonner sur le même problème, (plus le nombre est grand, plus on risque de perdre de temps sur la coordination) et de la qualité du cahier des charges. Evidemment, si le problème est classique, il existe un grand nombre de modules déjà existants, permettant de résoudre la plupart des problèmes sous-jacents. La qualité du travail de coordination est déterminante.

3.1.3.2 Au niveau tactique

Considérons maintenant le niveau du programmeur. Il vient de recevoir une description complète du travail à effectuer, avec un délai de livraison qui lui paraît évidemment trop court. Avec une méthode descendante, il va se trouver, une fois la moitié du temps écoulé, avec un prototype qui fait presque ce qu’il faut. Alors, s’il est sage, il réécrit son programme à partir de zéro avec l’expérience acquise. Il aboutit alors rapidement à une version correcte, et il peut consacrer le temps qui reste à la vérification de son programme. C’est une phase essentielle. Le programme ne vaut rien sans cette phase. Il faut de plus que durant la durée de son travail, il ait ébauché au moins trois niveaux de documentation de son travail :

niveau extérieur : une documentation rapide, permettant à un non spécialiste de comprendre de quoi il s’agit (Cette partie doit pouvoir éventuellement être lue par les gens d’un service commercial, ou par toute personne ayant un regard sur le travail, sans être un spécialiste).
niveau utilisateur : une description assez complète des parties avec toutes les fonctionnalités demandées par le cahier des charges. C’est le manuel de l’utilisateur.
niveau développeur : la description de tous les types abstraits utilisés ou de toutes les classes, et de toutes les particularités de programmation de bas niveau. Cette partie peut s’inscrire directement dans le code avec les javadocs par exemple. Elle est nécessaire parce que le projet peut commencer avec une équipe et finir avec une autre. Il faut aussi se rendre compte qu’au bout de trois semaines, on a oublié les « ruses » de programmation que l’on a utilisées, et la maintenance s’en trouve particulièrement difficile.

Attention ! Ne noyons pas les lecteurs de ces rapports sous un flot d’informations ne les concernant pas. Il faut savoir rester concis. Par exemple au niveau du développeur, quelques commentaires bien choisis peuvent suffire si le deuxième niveau a été bien conçu.

Pour illustrer, je me permets de citer J. F. Kennedy, qui refusait tout rapport de plus de dix lignes. En effet, il avait des collaborateurs qui devaient être capables de faire des synthèses pour lui, parce qu’il n’avait certainement pas le temps de se plonger dans tous les problèmes de sa nation.

Cet effort de synthèse n’est pas facile : résumer plusieurs mois de travail en moins de dix lignes demande une grande discipline. Pourtant, si c’est essentiel pour le lecteur, c’est aussi très utile pour fixer les notions de notre programmeur et pour l’aider à mieux se comprendre lui-même. Un utilisateur potentiel doit pouvoir, d’un seul coup d’œil, décider si le programme est adapté à son besoin.

D’expérience, un prototype défectueux (résultats défectueux dans 20% des cas) correspondant à trois mois de travail, s’il est bien documenté, peut être réécrit en moins d’une semaine en un programme qui fonctionne à un taux d’erreur minimal.

3.1.4 Des modules

Pour regrouper les notions qui correspondent aux objets d’un type, il faut les décrire dans un fichier unique. En fait, à chaque type (ou classe en programmation objet) doit correspondre :

un constructeur, c’est à dire une fonction qui crée la structure de l’objet à partir des valeurs de ses champs.
Une fonction d’accès à chacun des champs de la structure.
Les fonctions (ou méthodes pour l’objet) de traitement spécifiques à ce type

Prenons un exemple : nous avons besoin de décrire des personnes par leur nom, leur prénom et leur date de naissance. En Pascal, cela donnerait Exemple 3.1.4.1 et Exemple 3.1.4.2 :

  type
    date=record
             jour:[1..31];
             mois:[1..12];
             annee:integer;
           end;
  function cons_date(jour:[1..31];
                     mois:[1..12];
                     annee:integer)
                    :date;
  var
    d:date;
  begin
    d.jour:=jour;
    d.mois:=mois;
    d.annee:=annee;
    return(date)
  end;
  function jour(d:date):[1..31];
  begin
    return(d.jour)
  end;
  function mois(d:date):[1..12];
  begin
    return(d.mois)
  end;
  function annee(d:date):integer;
  begin
    return(d.annee)
  end;

Exemple 3.1.4.1 constructeur de dates (Pascal)

type
  personne=record
             nom,prenom:string;
             naissance:date;
           end;
function cons_personne(nom,prenom:string;
                       naissance:date)
                      :personne;
var
  p:personne;
begin
  p.nom:=nom;
  p.prenom:=prenom;
  p.naissance:=naissance;
  return(p)
end;
function nom(p:personne):string;
begin
  return(nom)
end;
function prenom(p:personne):string;
begin
  return(prenom)
end;
function naissance(p:personne):date;
begin
  return(naissance)
end;

Exemple 3.1.4.2 constructeur de personnes (Pascal)

Vous noterez dans cet exemple qu’on est obligé de définir le type date. On utilise évidemment exactement la même méthode. On pourrait croire que tout cela est inutile. Mais si par la suite, on décidait de modifier la structure de la date pour la coder sous la forme d’un entier unique contenant toute l’information, il suffirait d’écrire :

type
  date=integer;
function cons_date(jour:[1..31];
                   mois:[1..12];
                   annee:integer)
                  :date;
begin
  return((jour - 1) +
         31 * ((mois-1) +
               12 * annee))
end;
function jour(d:date):[1..31];
begin
  return((d mod 31) + 1)
end;
function mois(d:date):[1..12];
begin
  return(((d div 31) mod 12) + 1)
end;
function annee(d:date):integer;
begin
  return((d div 31) div 12)
end;

Exemple 3.1.4.3 constructeur de date modifié (Pascal)

La structure est physiquement différente. Une date occupe un entier (4 octets) au lieu de trois (12 octets), mais en contrepartie, le traitement est légèrement plus complexe. Peut-être que le calcul est aussi rapide, peut-être que l’économie de place mémoire est essentielle pour le fonctionnement de l’ensemble. La seule chose importante à retenir est que le changement d’implémentation de la date n’a pas la moindre répercussion sur le reste du code dans la limite où les autres éléments du programme accèdent aux données par les fonctions jour, mois et annee. Les autres programmeurs utilisant le type personne n’ont même pas besoin d’être prévenus.

La conception modulaire est imposée par la programmation objet et donc, tout cela ne semblera pas surprenant aux habitués de Java ou même de C++. Par contre, pour les autres développeurs, nous avons ici un bon exemple d’encapsulation d’une structure permettant de revoir l’implémentation plus tard de manière totalement transparente pour les autres utilisateurs.

Pour les développeurs Java, il s’agit d’utiliser les interfaces là où elles sont utiles.

Maintenant, développons encore un peu ce thème dans l’exemple suivant en C :

typedef enum {
  Tsphere,
  Tpave
} e_forme;
/* on peut rajouter d’autres
   formes ad lib */
typedef struct {
  t_point origine;
  float rayon;
} t_sphere;
typedef struct {
  t_point origine;
  t_vecteur v[3];
  /* pour les trois arêtes */
} t_pave;
typedef union {
  t_sphere sphere;
  t_pave pave;
} u_forme;
typedef struct {
  e_forme type_de_forme;
  u_forme donnees_forme;
}*t_forme;

Exemple 3.1.4.4 type de forme (C)

Nous avons supposé l’existence des types t_vecteur et t_point.

Nous avons ici un exemple d’utilisation des unions de types en C. Il est possible de représenter la même chose en Pascal grâce à la structure "record case of". Il a fallu choisir entre une structure ou une référence. J’ai choisi la référence. Il nous faut évidemment décrire d’une part les constructeurs cons_sphere et cons_pave qui devront en conséquence allouer l’espace mémoire nécessaire et d’autre part toutes les fonctions qui permettent d’accéder aux informations. Il se trouve que pour accéder aux informations, il nous faut connaître la nature de la forme : en effet, si origine est un champ commun aux deux structures représentées, ça n’a pas de sens de parler du rayon d’un pavé ou d’une arête d’une sphère, d’où le champ type_de_forme de la structure finale. Voyons comment programmer le reste du type abstrait en C :

t_forme cons_sphere(t_point origine,
                    float rayon) {
  t_forme res=(t_forme)malloc(sizeof(res*));
  res->type_de_forme=Tsphere;
  res->donnees_forme.sphere->origine=origine;
  res->donnees_forme.sphere->rayon=rayon;
  return res;
}
t_forme cons_pave(t_point origine,
                  t_vecteur v[3]) {
  t_forme res=(t_forme)malloc(sizeof(res*));
  int i;
  res->type_de_forme=Tpave;
  res->donnees_forme.pave->origine=origine;
  for (i=0;i<3;i++)
    res->donnees_forme.pave->v[i]=v[i];
  return res;
}

Exemple 3.1.4.5 constructeurs de t_forme (C)

Nous avons ici défini une structure qui correspond à une implémentation « objet » en C. Le langage C++ transforme ces classes d’une manière très similaire. Là encore, c’est l’état d’esprit de l’objet qui prime sur le langage utilisé, mais disons nous que dans un langage de bas niveau comme le C, il nous faut tout programmer à la main. Voyons quand même comment on aurait pu décrire l’ensemble avec l’aide d’un langage objet nous proposant l’héritage pour exprimer le fait que les sphères et les pavés bien que différemment structurés restent des formes :

Dans le fichier Forme.java :

public class Forme {
}

Dans le fichier Sphere.java :

public class Sphere extends Forme {
  public Point origine;
  public int rayon;
  public Sphere(Point origine,
                int rayon) {
    this.origine=origine;
    this.rayon=rayon;
  }
}

Dans le fichier Pave.java :

public class Pave extends Forme {
  public Point origine;
  public Vecteur v[3];
  public Pave(Point origine,
              Vecteur v[]) {
    this.origine=origine;
    for (int i=0;i<3;i++) {
      this.v[i]=v[i];
    }
  }
}

Exemple 3.1.4.6 forme revue (Java)

Ce n’est pas vraiment le choix d’implémentation que je ferai pour manipuler effectivement des formes, mais cela illustre simplement l’utilisation de l’héritage. Je préférerai définir Forme en tant qu’interface, mais il faudrait avoir un vrai exemple de problème à résoudre pour programmer ces classes. Sinon, je suis en flagrant délit de conception ascendante ! En effet, je propose ces objets dans le vide le plus total.

3.2 La récursivité

La méthode de loin la plus puissante pour concevoir un algorithme découle du théorème de la récurrence. Ceux qui ne la pratiquent pas, vous diront que son implantation est inefficace^³⁵. Ceux qui la pratiquent trouvent que tous les problèmes sont simples. Même, ils programment des solutions de problèmes qu’ils ne savent a priori pas résoudre !

3.2.1 Le concept

3.2.1.1 Le théorème de la récurrence

Nous avons défini le type entier avec l’opération Successeur dans le Type abstrait 2.2.1.2. Nous disposons par construction de la propriété suivante : tout entier non nul a un prédécesseur sauf Zéro. Nous savons aussi que toute partie non vide de cet ensemble admet un plus petit élément. Les hypothèses sont :

P(Zéro)
" n Î Entier, P(n) Þ P(successeur(n))

Supposons non vide l’ensemble des entiers tels que non P, cet ensemble admet donc un plus petit élément q. Cet élément serait alors non nul grâce à la première hypothèse. Son prédécesseur ne serait pas dans l’ensemble, donc il vérifierait P. En vertu de la deuxième hypothèse, on aurait alors P(q), ce qui infirme la supposition que cet ensemble est non vide. Nous disposons donc de la propriété : P(n) pour tout n appartenant à entier.

C’est un résultat simple mais extrêmement puissant conceptuellement. Bien utilisé, il nous permettra de déplacer des montagnes. Tout cela repose sur le fait que l’on n’arrive pas à trouver de point de départ aux entiers qui ne vérifient pas la propriété.

3.2.1.2 Amorcer la pompe

P(Zéro)

Donnez moi un point fixe et je soulèverai le monde... Comme pour une mayonnaise, il faut mettre de l’œuf au départ. La première hypothèse est indispensable. C’est la base du raisonnement. Sans cette vérité initiale, tout programme tourne dans le vide. A un moment ou un autre, il faut amorcer la pompe. Souvenez-vous, on peut démontrer que pour tout ensemble de cardinal quelconque, tous les éléments sont égaux. La seule infirmité de la démonstration se situe dans la nécessité de la propriété de base au rang 2 pour démontrer l’hypothèse de récurrence :

Raisonnement récursif erroné

Figure 3.2.1.1 raisonnement récursif erroné

Pour la démonstration, on suppose que la propriété est vraie au rang n et on conçoit un ensemble de cardinal n+1. Comme on peut le partitionner de deux manières et que l’égalité est transitive, on a bien l’égalité de tous les éléments de l’ensemble. Avec un peu plus de réflexion, on verra que pour cela, l’intersection des deux ensembles de n éléments doit être non vide. Donc l’hypothèse de récurrence n’est vraie qu’à partir du rang 2. Il nous faudrait donc avoir comme hypothèse de départ que 2 éléments dans un ensemble sont égaux, ce qui est heureusement faux.

Revenons-en donc à nos moutons.

A cause de leur habitude des méthodes itératives, les programmeurs parlent souvent par erreur de test d’arrêt, voir de clause d’arrêt. Evidemment, il s’agit d’une clause de départ. Nous parlerons désormais de base de la récurrence ou de clause initiale. Même si son évaluation intervient souvent en dernier, c’est le point de départ du raisonnement.

3.2.1.3 Lancer la mécanique

" n Î Entier, P(n) Þ P(successeur(n))

La seconde partie, nommée habituellement hypothèse de récurrence^³⁶, n’est par contre jamais oubliée. Parfois pourtant, elle est mal gérée par ceux qui ont l’habitude des raisonnements itératifs et impératifs. C’est presque toujours parce qu’ils cherchent un savant mélange des deux. Choisissez la solution 100% récursive si vous en avez les moyens. Si cette hypothèse est bien gérée, elle suffit à décrire tous les autres cas et il n’est pas nécessaire de créer de cas particuliers.

3.2.2 Méthodes pratiques

Pour ceux qui ont un lourd passé d’itératif, il est parfois difficile d’accepter la puissance du récursif, mais il est toujours difficile de remettre en question des années de travail. Voici donc quelques méthodes d’aide à la conception :

3.2.2.1 Jamais de cas particulier

Voici l’exemple du calcul de la longueur d’une liste en Pascal, C et Lelisp. Il s’agit bien entendu d’un exemple simpliste, mais il illustre bien notre propos :

function longueur(l:liste):integer;
begin
  if vide(l) then
    return(0)
  else
    return(1+longueur(suite(l)))
end;

Exemple 3.2.2.1 calcul de la longueur d’une liste (Pascal)

Notez au passage l’absence de point-virgule entre le begin et le end. Il n’y a qu’une seule instruction de chaque niveau. S’il y a un point-virgule en Pascal, cela marque l’existence de deux instructions de même niveau à la suite, ce qui signale un effet de bord (nous y reviendrons plusieurs fois).

int longueur(liste *l)
{
  if (vide(l))
    return(0);
  else
    return(1+longueur(suite(l)));
}

Exemple 3.2.2.2 calcul de la longueur d’une liste (C)

Le else n’est pas indispensable car l’évaluation s’arrête au return, mais il ne coûte rien en temps d’exécution et donne une certaine symétrie qui permet d’éviter beaucoup d’erreurs de débutant.

(de longueur (l)
   (if (vide l)
       0
       (+ 1 (longueur (suite l)))))

Exemple 3.2.2.3 calcul de la longueur d’une liste (Lelisp)

Dans le cas simple du calcul de la longueur d’une liste (Exemple 3.2.2.1, Exemple 3.2.2.2 et Exemple 3.2.2.3), la longueur de la liste nulle n’est pas un cas particulier. Il s’agit d’une expression qui sera évaluée pour toutes les listes, quelque soit leur longueur. Il ne faudrait pas, par exemple, écrire dans la clause de base de la version Pascal, writeln(‘La liste est vide’), car le message serait imprimé pour toutes les listes. Il ne faut pas inclure de cas particulier dans notre fonction récursive. S’il s’agit d’un cas particulier, c’est un cas rare. Il n’est donc pas nécessaire de vérifier à chaque retour dans la fonction si on se trouve dans ce cas particulier. C’est une perte de temps et non un gain. De plus, il devient difficile de cerner véritablement ce qui est nécessaire au fonctionnement. Notez au passage que les fonctions sont (au sens mathématique) définies partout. C’est-à-dire que dans tous les cas il y a un return ou une valeur quelconque à rendre. Nous avons évité l’erreur classique d’oublier de rendre une valeur pour la clause de base.

Notez au passage que je ne donne pour l’instant aucun exemple en Java car, le type Liste y est déjà implémenté avec toutes les fonctions nécessaires et que le choix de la structure sous-jacente n’est pas les listes chaînées (ce qui n’a pas d’impact sur les fonctionnalités, mais sur l’efficacité).

3.2.2.2 Programmer « optimiste »

Pour que notre fonction soit correcte, il faut partir du principe qu’elle est correcte ! Cette affirmation choque votre sens de la logique ? C’est normal, mais cet « optimisme » n’est pas injustifié. Exprimons plutôt le problème sous la forme suivante : quelque soit le problème, exprimer la valeur pour le rang n demande de supposer que la fonction considérée est capable d’évaluer jusqu’au rang n-1, puis de définir la valeur du rang n en fonction de la valeur du rang n-1. C’est purement déclaratif : on définit une valeur et on laisse la machine trouver l’ordre d’évaluation et évaluer. Dans le cas des listes que nous avons évoqué dans l’Exemple 3.2.2.1 et l’Exemple 3.2.2.3, il suffit d’exprimer la valeur de longueur de la liste en fonction de la longueur de sa suite : longueur(L) est exprimée comme 1 + longueur(suite(L)) Cela paraît trop simple pour être vrai, la première fois, mais on s’y habitue. On développe de plus en plus vite et avec beaucoup de sûreté. La fonction est correcte par construction, en vertu du théorème de la récurrence.

3.2.3 Modèles de fonctions récursives

En fait, presque toutes les fonctions récursives dérivent d’un des deux modèles suivants. Beaucoup d’autres dérivent indirectement du modèle mutuellement récursif que je cite donc à titre de curiosité intellectuelle. Par contre, j’évite sciemment les tours de Hanoi qui sont souvent citées comme cas d’école, mais qui ne sont jamais qu’un cas d’école justement.

3.2.3.1 Le modèle non terminal

Je choisis comme modèle la fonction append Les calculs se font à la fin. Comme pour le calcul de la longueur présenté dans l’Exemple 3.2.2.1, la concaténation naturelle de deux listes chaînées demande que le calcul ait déjà été fait sur la suite. Voyons l’exemple en Lelisp :

(de append (l1 l2)
    (if (vide l1)
        l2
        (cons (tete l1)
              (append (suite l1) l2))))

Exemple 3.2.3.1 concaténation de deux listes (Lelisp)

Si on déroule mentalement le mécanisme d’évaluation pour l’expression

(append ’(a b c) ’(d))

l’interprète décompose en

(cons ’a (append ’(b c) ’(d))

puis

(cons ’a (cons ’b (append ’(c) ’(d))))

puis

(cons ’a (cons ’b (cons ’c (append () ’(d)))))

et il peut enfin commencer à évaluer successivement de l’intérieur vers l’extérieur :

(cons ’a (cons ’b (cons ’c ’(d))))

(cons ’a (cons ’b ’(c d)))

(cons ’a ’(b c d))

pour finir avec (a b c d) qui est bien la liste que nous attendions. Il ne nous est pas nécessaire de comprendre ce fonctionnement pour savoir que la valeur que nous exprimons sera correcte.

3.2.3.2 Le modèle terminal

Ici le modèle sera la fonction auxiliaire de l’inversion de liste, reverse_aux. C’est vraiment la première fonction récursive terminale que l’on rencontre dans la pratique. L’inversion de listes se fait assez naturellement en passant par une fonction auxiliaire qui fait les calculs au fur et à mesure, sur ses arguments :

(de reverse (l)
  (reverse-aux l ()))
(de reverse-aux (l r)
  (if (vide l)
      r
      (reverse-aux (suite l)
                   (cons (tete l) r))))

Exemple 3.2.3.2 inversion de liste (Lelisp)

Voyons l’évaluation de l’expression (reverse ’(a b c)) :

L’interprète l’évalue successivement à

(reverse-aux ’(a b c) ())

(reverse-aux ’(b c) ’(a))

(reverse-aux ’(c) ’(b a))

(reverse-aux () ’(c b a))

qui vaut effectivement (c b a) comme on le voulait^³⁷. Vous notez qu’aucun calcul n’est en attente. Les calculs sont donc bien effectués au fur et à mesure. Cela veut dire en terme d’évaluation qu’il n’est pas nécessaire d’empiler de nouveaux environnements locaux. En terme d’évaluation, ce genre de fonction est aussi efficace sinon plus que l’équivalent en itératif.

3.2.3.3 Deux fonctions mutuellement récursives

Nous voilà avec deux fonctions qui sont définies l’une en fonction de l’autre. La circularité évidente est contournée dans l’exemple suivant en Pascal par l’emploi du mot clé forward.

function impair(n:integer):boolean;
  forward ;
function pair(n:integer):boolean;
begin
  return(n=0 or impair(n-1))
end;
function impair(n:integer):boolean;
begin
  return(n<>0 and pair(n-1))
end;

Exemple 3.2.3.3 parité d’un entier naturel (Pascal)

Nous avons là un exemple mutuellement récursif terminal car aucune évaluation ne reste en suspens. Les fonctions s’appellent l’une l’autre en décrémentant leur argument à chaque étape jusqu’à ce qu’une des deux arrive sur zéro. C’est celle là qui rendra false si c’est impair et true si c’est pair.

Voyons quand même un autre exemple non terminal celui-là : il s’agit de deux fonctions permettant de distribuer les éléments d’une liste en deux parts, la liste des éléments de rang pair et la liste des éléments de rang impair.

(de rg-pair (l)
    (if (vide l)
        ()
        (rg-impair (suite l))))
(de rg-impair (l)
    (if (vide l)
        ()
        (cons (tete l)
              (rg-pair (suite l)))))

Exemple 3.2.3.4 un élément sur deux (Lelisp)

L’appel de rg-pair dans la définition de rg-impair est non terminal car il reste un cons en suspens.

L’évaluation de ces fonctions là mérite un petit exemple :

(rg-pair ’(a b c d))

(rg-impair ’(b c d))

(cons ’b (rg-pair ’(c d))

(cons ’b (rg-impair ’(d))

(cons ’b (cons ’d (rg-pair ())))

qui peut en fin être évalué :

(cons ’b (cons ’d ()))

(cons ’b ’(d))

(b d)

Inversement pour l’autre fonction :

(rg-impair ’(a b c d))

(cons ’a (rg-pair ’(b c d))

(cons ’a (rg-impair ’(c d))

(cons ’a (cons ’c (rg-pair ’(d))

(cons ’a (cons ’c (rg-impair ())))

qui peut en fin être évalué :

(cons ’a (cons ’c ()))

(cons ’a ’(c))

(a c)

Ces deux fonctions nous serviront pour le tri fusion, Exemple 5.1.1.10

Nous écrirons aussi des fonctions mutuellement récursives dans l’Exemple 5.1.1.15 tri interclassement monotone de liste (Lelisp).

4 Les grandes familles d’optimisations

On cherche en permanence à améliorer les performances d’un programme. Il s’agit en général de le rendre plus rapide. Si on tient compte de la rapidité croissante des machines et des progrès considérables en matière de génération automatique de code, toutes les formes d’optimisations ne sont pas utiles, et toutes n’ont pas à être faites par le programmeur. Voici l’essentiel de ce qui peut être fait.

4.1 L’optimisation de l’algorithme

Ce type d’optimisation ne peut que très rarement être fait automatiquement. C’est donc sur ce point que l’on se concentre en particulier. Evidemment, il faut avoir fait tourner un prototype pour pouvoir déterminer l’utilité de telle ou telle optimisation. Il sera évidemment inutile de consacrer du temps de développement à des portions négligeables du calcul.

Il faut savoir déterminer les éléments coûteux du programme. Si un calcul prend 2% du temps, même si on peut diviser sa durée par 10, cela ne présente pas vraiment d’intérêt. Par contre si un traitement consomme 40% de la place mémoire utilisée et que justement, c’est l’espace mémoire qui fait défaut, il suffira peut-être de diviser cette consommation par deux pour ne plus nécessiter de « swap » lors de l’exécution dans les cas pratiques courants.

Nous allons étudier quelques méthodes pour diminuer la durée des traitements.

4.1.1 Rapprocher l’information de la racine

4.1.1.1 Des listes aux arbres

Si on a travaillé sur un type abstrait représentant un ensemble de données implanté sous forme de listes statiques^³⁸ ou dynamiques^³⁹ (c’est le cas 95% du temps), on obtient des complexités de parcours de recherche en n, la taille de la liste. Les algorithmes qui en découlent ont des complexités en n ou pire... Cela vient du fait que les informations sont loin de la « racine ». Il faut en moyenne n/2 (bref, de l’ordre de n) opérations pour atteindre un élément quelconque de la liste.

C’est là que vient l’idée des arbres. Il s’agit intuitivement de rapprocher les informations de la racine (c’est-à-dire de la première cellule, celle à partir de laquelle on accède aux autres). Un arbre binaire de profondeur n contient 1+2+4+...+2ⁿ=2ⁿ⁺¹-1 informations sur ses nœuds. Donc un arbre binaire (équilibré) contenant N nœuds a une hauteur approximative de log₂(N). Ce qui signifie en clair que les informations sont en moyenne à une distance de l’ordre de log₂(N) de la racine. Les algorithmes que l’on pourra définir sur ce type de structure, seront d’un ordre de grandeur nettement inférieur.

Il ne s’agit pas de diviser le temps de calcul par 2, par 10 ou mieux, il s’agit de permettre des calculs avec des données immenses là où d’autres algorithmes ne pourraient tout simplement pas aller.

L’amélioration algorithmique se fait au détriment du temps de mise au point et sous la réserve qu’elle soit adaptée au problème (pour les listes triées ou les arbres binaires de recherche, il faut que les éléments soient munis d’une relation d’ordre totale).

4.1.1.2 Des arbres aux tables de hachage

Une fois de plus, on peut améliorer notre temps d’accès à l’information, si on trouve une bonne fonction de hachage (cf. section 5.1.3). On va mettre tous nos objets à la racine ! (Grossièrement, avec les listes, les objets sont en moyenne à une distance de n, avec les arbres binaires, à log₂(n) et avec les tables de hachage, ils sont tous à 1).

On met tous nos objets dans un tableau et on trouve une bijection simple entre les indices du tableau et nos objets. Sous réserve d’une bonne résolution des collisions (cf. 5.1.3.4), on peut arriver à obtenir une fonction qui donne en une seule opération, l’indice dans un tableau d’un objet accessible par une clé.

Le classement de ces objets devient alors une opération en temps constant, et la recherche aussi !

Cette méthode est utilisable dans une multitude de cas (Il ne faut pas par contre, que l’on veuille maintenir une équivalence entre l’ordre des éléments et l’ordre des indices). On peut ainsi représenter, des ensembles, des listes et même des arbres quelconques^⁴⁰.

4.1.2 Factoriser les calculs : les mémofonctions, la cache

Prenez un être humain quelconque. Mettez-le face à une cuisinière électrique, et demandez lui de mettre la main sur une des plaques encore chaude.

La première fois, il est possible qu’il se brûle. Mais vous ne l’aurez pas deux fois.

Pourquoi un programme devrait-il être trop bête pour mémoriser un évènement et s’en resservir ? Demandons au même opérateur humain, une fois guéri et muni d’une feuille de papier, de calculer le factoriel de 7. Au bout d’un certain temps, il propose un résultat (avec un peu de chance, il vous propose 5040).

Si vous lui demandez ensuite le factoriel de 5, il vous répond sans calcul, 120. De même, il ne lui faut qu’un seul calcul pour assurer que le factoriel^⁴¹ de 8 est 40320.

Quel miracle s’est-il produit ? Tout est sur sa feuille de brouillon ! C’est l’idée des mémofonctions. Le programmeur va utiliser une structure de données adaptée qui va lui permettre de sauvegarder les calculs déjà effectués pour pouvoir éviter de les refaire.

Attention ! L’opération de recherche des calculs déjà connus ne doit pas coûter plus cher que le calcul lui-même. Pour cela, il faudra utiliser une structure à accès direct (tableau ou table de hachage).

C’est ce genre d’opération qui est réalisé sous le nom de cache pour Internet par exemple. Lorsqu’un individu accède pour la première fois à une page d’un site, celle-ci est recopiée en plusieurs points de la toile. S’il retourne consulter cette page, ou si un autre utilisateur y accède, il ne sera pas nécessaire d’aller relire la page sur le site d’origine : une des copies suffira.

Voyons l’exemple simpliste du factoriel. L’idée générale est de sauvegarder tous les résultats intermédiaires des calculs de factoriels, sachant que pour calculer n!, nous aurons mémorisé toutes les valeurs de factoriels entre 0 et n.

Pour démarrer, il suffit de mettre l’information de départ, 0!=1 dans notre table, et par la suite pour calculer un nouveau factoriel, il suffira de partir du dernier factoriel connu et d’effectuer le calcul, d’une part pour le rendre, mais aussi pour le stocker dans l’ensemble des factoriels connus.

type
  table_de_factoriel=record
    t:array[0..Max] of integer;
    n:integer;
  end;
var
  table:table_de_factoriel;
function factoriel(n:integer):integer;
var
  res:integer;
begin
  if n<=table.n then
    return(table.t[n])
  else
    begin
      fact:=n*factoriel(n-1);
      table.n=n;
      table.t[n]=fact;
      return(fact)
    end
end;

Exemple 4.1.2.1 factoriel intelligent (Pascal)

Notez que dans le cas du factoriel, je n’ai pas besoin d’une table de hachage car les arguments sont déjà des indices et sont en plus calculés gentiment dans le bon ordre.

Profitons quand même de l’occasion pour montrer la structure de tables de hachage proposée par Lelisp : les plist (property list).

(plist ’factoriel ’(0 1)) ;on stocke 0!=1
(de factoriel (n)
    (cond ((getprop ’factoriel n))
          ((putprop ’factoriel
                    (* (factoriel (- n 1))
                       n)
                    n))))

Exemple 4.1.2.2 factoriel intelligent (Lelisp)

Il se trouve que le factoriel est un bon exemple dans la limite où il est simple mais que c’est un mauvais exemple dans le sens où il n’y a pas de gain véritable en temps car le nombre de factoriels que l’on arrive à calculer sans dépasser les limites des entiers dépasse à peine les 20.

C’est beaucoup plus intéressant pour l’exemple de la suite de Fibonnacci. Pour calculer fib₁₀ qui vaut 89, il faut 89 appels en théorie ce qui est encore acceptable alors que pour fib₁₀₀, il faut de l’ordre de 10²⁰ appels et les arrondis successifs empêchent le calcul d’être précis^⁴². Voici d’abord la version classique en Java :

int fibonacci(int n) {
  if (n==0) {
    return 1;
  } else if (n==1) {
    return 1;
  } else {
    return fibonnacci(n-1)+
           fibonnacci(n-2);
  }
}

Exemple 4.1.2.3 fibonnacci sans mémoire (Java)

Cette version atteinte de la maladie d’Alzheimer prend donc un temps quasi infini pour calculer fib₁₀₀ avec une imprécision digne de l’aveugle décrivant les différentes nuances des tons d’un coucher de soleil. La version suivante réalise le calcul en 100 appels successifs sans aucun problème d’arrondis autre que l’imprécision naturelle des entiers de la machine :

//d’abord créer la structure (en ayant importé
//la classe java.util.Hashtable
private static Hashtable table=new Hashtable();

//puis mettre les valeurs de fib(0) et fib(1)
//dans cette table
static {
table.put(new Integer(0),new Integer(1));
table.put(new Integer(1),new Integer(1));
}

Notez qu’il n’est pas possible d’utiliser directement les int pour les clés et les valeurs. C’est pourquoi nous en faisons des objets Integer avec un "new".

int fibonnacci(int n) {
  if (table.containsKey(new Integer(n)))
    return ((Integer)table.get(new
                      Integer(n))).intValue();
  else {
    Integer res=new Integer(fibonnacci(n-1)+
                            fibonnacci(n-2));
    table.put(new Integer(n),res);
    return res.intValue();
  }
}

Exemple 4.1.2.4 fibonnacci intelligent (Java)

Là encore nous subissons une certaine lourdeur de la classe de base Hashtable qui n’est pas faite pour stocker des int mais des objets plus lourds repérés par des clés de type String : nous sommes contraints de faire des conversions de type explicites. Nous aurions pu utiliser un tableau simple, mais j’avais envie de montrer un exemple utilisant des tables de hachage.

Voyons quand même l’exemple en Lelisp qui brille par sa concision :

(plist ’fibonnacci ’(1 1 0 1))
(de fibonnacci (n)
    (cond ((getprop ’fibonnacci n))
          ((putprop ’fibonnacci
                    (+ (fibonnacci (- n 1))
                       (fibonnacci (- n 2)))
                    n))))

Exemple 4.1.2.5 fibonnacci intelligent (Lelisp)

4.1.3 Faire les calculs à l’avance

Dans l’Exemple 4.1.4.1, il pourrait être utile de calculer à l’avance un maximum de nombres premiers pour éviter d’avoir à les calculer dynamiquement^⁴³. On peut évidemment en calculer un grand nombre une fois pour toute et les mettre en clair dans les sources du programme.

C’est la solution retenue par les canadiens qui ont programmé les premières versions du célèbre logiciel de calcul formel Maple, qui contient tous les nombres premiers inférieurs à 1000 précalculés pour accélérer de nombreux calculs. De plus, s’il est nécessaire d’en calculer d’autres, ils sont évidemment mémorisés.

4.1.4 Eviter les calculs inutiles

4.1.4.1 Evaluation à la demande

Calculer d’avance et éviter les calculs inutiles sont deux stratégies qui semblent antinomiques, mais c’est une apparence : on calcul d’avance ce que l’on est sûr d’utiliser et on fait de l’évaluation retardée (lazy evaluation) sur les portions dont on est moins sûr. En particulier, on peut parfois factoriser l’allocation et la libération de mémoire. On peut mettre en suspend la libération d’un ensemble de cellules en vue de les réutiliser directement lors d’une allocation ultérieur. On peut aussi suspendre l’allocation effective d’un espace mémoire tant que l’utilisateur n’y fait pas d’accès explicite.

Dans le cas de nos mémofonctions, il va falloir faire des compromis.

Un bon exemple, celui des nombres premiers : dans l’exemple de la décomposition de « grands » nombres en vue du calcul de leur factoriels, on manipule la liste infinie des nombres premiers. Il serait de très mauvais goût de se mettre à la calculer.

On pourrait, par contre, décider une fois pour toute que le programme n’utiliserait que les cent premiers. On pourrait alors les mettre dans un tableau et ne plus en parler. Le drame, c’est qu’il ne sont peut-être pas tous utiles et que peut-être qu’il n’y en a pas assez...

Par contre dans l’exemple des combinaisons, on n’a besoin du nombre premier que lorsqu’on a déjà utilisé les précédents. Pour y mettre un semblant de rigueur, on se sert des nombres premiers sous la forme du type abstrait suivant :

Sorte : Nombre_premier

Opérations :

suivant : Nombre_premier ® Nombre_premier
premier_des_premiers : ® Nombre_premier

(C’est 2 pour nous en l’occurrence en tant que premier diviseur intéressant)

Type abstrait 4.1.4.1 nombres premiers

C’est une boîte noire de maniement extrêmement simple. Maintenant, si on veut pouvoir rester efficace, sachant que ces nombres premiers vont être souvent sollicités, on peut implanter ce type abstrait sur la base d’une variable globale : la liste des nombres premiers connus (du programme).

On écrit alors une mémofonction, qui ne rajoute de nombres premiers dans sa base qu’à la demande.

La liste infinie des nombres premiers se laisse alors manipuler comme si elle n’était qu’une simple liste finie. Voyons l’exemple en Lelisp :

(setq premier-des-premiers 2)
(setq liste-n-p-c
      (list premier-des-premiers))
; la liste des nombres premiers connus
(de suivant (npremier)
   (cond ((successeur npremier
                      liste-n-p-c))
          ; on le rend s’il existe
         (t (calcul npremier
                    liste-n-p-c))))
          ; sinon on le calcule

(de calcul (n l)
   (cond ((null l)
          (rajouter n)
          n)
          ; pas de diviseur donc
          ; on le met à la fin la liste
          ; et on le rend
         ((divisible n (tete l))
          (calcul (+ 1 n)
                  liste-n-p-c))
          ; on a un diviseur donc
          ; on essaie le suivant
         (t
          (calcul n (suite l)))))

Il nous manque la définition de successeur et de rajouter. Une fois de plus, c’est un autre type abstrait que nous devons implanter et plusieurs possibilités s’offrent à nous. Le choix du sens de stockage des nombres premiers par exemple. Voici une solution avec l’ordre décroissant :

(de rajouter (n)
  (setq liste-n-p-c
        (cons n
              liste-n-p-c))
(de successeur (n l)
  (cond ((vide (suite l))
         ())
        ((= (tete l) n)
         (tete (suite l)))
        (t (successeur n (suite l)))))

J’ai des solutions plus courtes et plus efficaces à proposer, mais elles utilisent des fonctions particulières de Lelisp comme nconc et je veux rester générique.

Exemple 4.1.4.1 les nombres premiers à la demande (Lelisp)

Maintenant, pour ceux qui pensent que cet algorithme naïf de recherche des entiers devrait être amélioré, je conseille un petit saut à la section 4.3.2.1, où est abordée la question.

4.1.4.2 Petits effets de bord

4.1.4.2.1 Mais que sont donc ces fameux « effets de bord » ?

Voici, pour commencer une définition rigoureuse des effets de bord : un effet de bord est une modification de l’environnement (sic).

Ce qui motive les interdictions abusives de ce genre de pratique, est la peur de la perte d’information^⁴⁴.

Pourtant, nos mémofonctions ne travaillent exclusivement qu’avec des effets de bord, et il ne s’agit pas d’une perte d’information, bien au contraire !

Avant tout, rappelons que les fonctions sont sensées rajouter une valeur à l’environnement. Les procédures par contre sont sensées, par essence, modifier l’environnement : soit l’environnement visuel de l’utilisateur (procédures d’affichage), soit l’environnement de calcul, en transformant la valeur de variables externes à la procédure ou de variables passées par référence (avec var en Pascal ou une structure référencée en C ou Java ou même en Lelisp par la modification du contenu d’une cellule avec les fonctions rplaca, rplacd et displace).

On essaie de n’utiliser que des fonctions plutôt que des procédures dans le but d’éviter la perte d’information^⁴⁵. On rajoute des informations dans notre environnement, sans les transformer ni les détruire. On ne manipule que des données cohérentes. Voici une des pratiques courantes à éviter : définir une donnée incorrecte pour la modifier par la suite et la rendre correcte. Il vaut mieux construire directement la bonne donnée. Si ce n’est pas possible, il faut créer une donnée intermédiaire d’un autre type. Le but étant de ne voir coexister dans votre programme, que des données correctes.

Par définition, toute affectation est un effet de bord. Bien sûr, les affectations ne sont pas conçues pour nous faire perdre de l’information. Mais observez bien vos programmes, et vous remarquerez qu’il n’y a que deux sortes d’affectations correctes :

l’initialisation (la variable reçoit sa première valeur, donc pas de perte d’information)
l’augmentation d’information (par exemple i:=i+1 ou plus généralement A:=f(A), où on utilise l’ancienne valeur de A pour l’enrichir).

Il est en effet rare de trouver une affectation a:=b où a avait une valeur effectivement utile. C’est souvent une erreur.

4.1.4.2.2 Comment s’en servir ?

On peut utiliser des effets de bord pour diriger l’évaluation. L’idée générale du type d’optimisation que nous allons étudier maintenant, est d’éviter le parcours de sous arbres d’évaluations complets, en transmettant de l’information de manière transversale à l’aide de variables globales (ou de variables de classe pour Java). En effet, lorsqu’on cherche à maximiser un critère, dès qu’on a un maximum local, il n’est plus nécessaire de chercher dans des cas qui ne peuvent rendre qu’une valeur inférieure.

Cela concerne une large famille d’algorithme de complexité exponentielle. Cela paraîtra beaucoup plus clair avec les trois exemples qui suivent : le problème du plus grand rectangle blanc, le calcul de la distance entre deux mots et les coupes αβ dans l’algorithme Min Max.

4.1.4.2.3 L’exemple du plus grand rectangle blanc

Le casse tête suivant me fût proposé par Robert Erra :

Etant donné un tableau de taille T x T contenant des cases noires et des cases blanches, trouvez la surface du plus grand rectangle inscrit dans le tableau qui ne contienne aucune case noire.

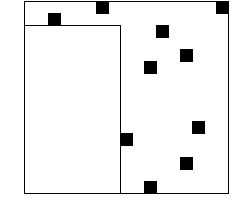
le plus grand rectangle blanc

Figure 4.1.4.1 le plus grand rectangle blanc

Les habitués de l’itératif trouvent relativement rapidement des méthodes (pas toujours très systématiques) qui permettent de faire croître un rectangle dans deux directions tant qu’on ne butte pas sur une case noire… Il faut donc essayer pour chaque case du tableau (T² étapes) un traitement qui demande aussi un parcours d’une surface donc de complexité T². Vous me direz immédiatement que la surface que l’on parcourt est beaucoup plus petite que le tableau. Je vous répondrai que si vous doublez la taille T, vous doublez la largeur et la hauteur de ce que vous parcourez, et dès lors, nous arrivons bien à une complexité de l’ordre de T⁴. Par des ruses diverses, on « améliore » le programme en descendant à T³ et en perdant la moitié des cas.

Arrêtons le massacre ! Nous allons ensemble caractériser la solution, ce qui nous donnera un algorithme en 4ⁿ où n est le nombre de cases noires. C’est beaucoup moins bien, mais nous le transformerons immédiatement en un programme de complexité n x log(n). Ce qui est beaucoup plus correct.

Notre fonction de recherche va d’abord prendre un rectangle en argument. Exprimer qu’un rectangle est maximal, c’est dire qu’il ne contient pas de cases noires. Ceci sera donc la base de notre récurrence.

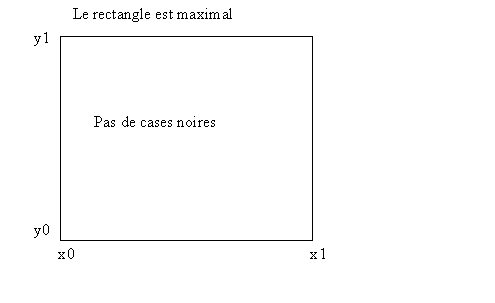
un rectangle maximal

Figure 4.1.4.2 un rectangle maximal

Si par contre, nous y trouvons une case noire, nous pouvons définir quatre zones susceptibles de contenir le rectangle maximal : au dessus, en dessous, à gauche et à droite. Il y a des recouvrements entre les zones, mais c’est indispensable.

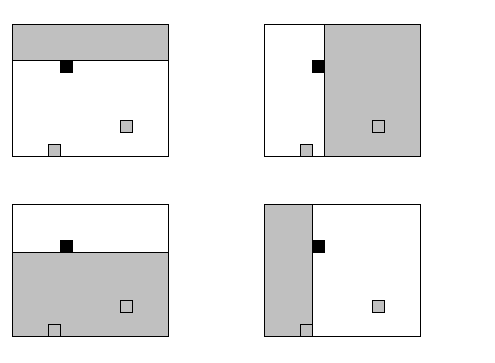
les quatre zones définies par une case noire

Figure 4.1.4.3 les quatre zones définie par une case noire

La solution de notre problème est obligatoirement dans une des quatre zones représentées en gris. Si on programme la fonction ainsi, pour chaque case noire trouvée, nous lançons quatre appels récursifs, ce qui nous donne l’épouvantable 4ⁿ dont nous parlions.

C’est évidemment impossible dès que nous dépassons une dizaine de cases noires. Mais par contre, nous avons un programme très simple et qui est sûr d’aboutir à la bonne valeur même si ce sera lors du quatrième millénaire. C’est ce type de programme que nous pouvons facilement optimiser.

Définissons donc une variable globale surface_maximale que nous initialisons à 0. Elle nous servira évidemment pour représenter le résultat de notre recherche, mais elle va aussi nous servir à ne lancer des recherches que dans des zones de surface supérieure à celle du dernier rectangle maximal trouvé.

rectangle(x0,x1,y0,y1) ne contient pas de case noire. Donc on affecte la nouvelle surface maximale qui est : surface(rectangle(x0,x1,y0,y1)) ce qui donne : surface_maximale:=(x1-x0+1)*(y1-y0+1)
rectangle(x0,x1,y0,y1) contient la case noire case(x,y). Donc on va relancer la recherche sur les quatre zones
- recherche(rectangle(x+1,x1,y0,y1))
- recherche(rectangle(x0,x-1,y0,y1))
- recherche(rectangle(x0,x1,y+1,y1))
- recherche(rectangle(x0,x1,y0,y-1)) dans la limite où ces zones sont de surface strictement supérieures à surface_maximale.

Le programme que nous allons maintenant proposer pour effectuer ce calcul ne nécessite pas la représentation du tableau lui-même. En effet, nous utiliserons la liste des cases noires pour représenter l’ensemble de nos données.

Je laisse imaginer au lecteur le développement des classes Case et Rectangle qui sont relativement simple. La méthode appartient de la classe Case vérifie simplement que les coordonnées de la case sont dans les intervalles du rectangle passé en argument.

Nous définissons la méthode recherche sur la classe principale PlusGrandRectangleBlanc :

import java.util.Vector;
import java.util.Iterator;
public class PlusGrandRectangleBlanc {
  public Rectangle rectangleDeDepart;
  public Vector listeDeCasesNoires;
  public PlusGrandRectangleBlanc() {
    //on mettra ici la saisie ou la
    //génération automatique de la liste
    //des cases noires et la saisie
    //des coordonnées du rectangle
    //de départ
  }

  /** la méthode rend null s’il n’y a
      pas de Case et la Case sinon */
  Case trouveUneCase(Vector listeDeCasesNoires,
                     Rectangle rectangle) {
    Iterator it=listeDeCasesNoires.iterator();
    Case res;
    while(it.hasNext()) {
      Case case=(Case)it.next();
      if(case.appartient(rectangle))
        return case;
    }
    return null;
  }

  /** notre variable globale */
  int surfaceMaximale=0;
  /** la méthode de recherche sera lancée sur
      rectangleDeDepart et rend la surface
      maximale. */
  int recherche(Rectangle rectangle) {
    Case case=trouveUneCase(listeDeCasesNoires,
                            rectangle);
    if (case==null) {
      surfaceMaximale=rectangle.surface();
      return surfaceMaximale;
    } else {
      int x0=rectangle.x0;
      int x1=rectangle.x1;
      int y0=rectangle.y0;
      int y1=rectangle.y1;
      int x=case.x;
      int y=case.y;
      Rectangle z1=new Rectangle(x+1,x1,y0,y1);
      Rectangle z2=new Rectangle(x0,x-1,y0,y1);
      Rectangle z3=new Rectangle(x0,x1,y+1,y1);
      Rectangle z4=new Rectangle(x0,x1,y0,y-1);
      if(z1.surface()>surfaceMaximale)
        recherche(z1);
      if(z2.surface()>surfaceMaximale)
        recherche(z2);
      if(z3.surface()>surfaceMaximale)
        recherche(z3);
      if(z4.surface()>surfaceMaximale)
        recherche(z4);
    }
  }
}

Exemple 4.1.4.2 recherche du plus grand rectangle blanc (Java)

De par la construction, notre problème est résolu. Pourtant, nous avons utilisé un effet de bord sur l’entier surfaceMaximale. Ce qui veut dire que pendant l’évaluation de la recherche sur la zone z1, la valeur de cet entier a pu changer plusieurs fois. Mais cette valeur ne peut que croître, car la recherche ne se fait que sur des surfaces strictement supérieures. En conséquence, l’évaluation de la recherche sur z1 va peut-être empêcher la recherche sur z2 qui est de surface inférieure.

Visualisons l’évaluation comme un arbre dont la racine est le rectangle de départ. Chaque nœud de cet arbre est une zone.

Si la zone est maximale (c’est-à-dire qu’elle ne contient aucune case noire), c’est une feuille de l’arbre (i.e. le nœud n’a pas de fils).

Si la zone n’est pas maximale, elle contient un point et le nœud a donc 4 fils.

L’arbre complet a donc un nombre de nœud de l’ordre de 4ⁿ où n est le nombre de cases noires. Nous cherchons la feuille la plus haute, celle qui représente la zone la plus grande.

Sans l’effet de bord qu’est l’affectation de notre variable globale, nous devrions visiter l’ensemble de cet arbre. Mais chaque visite à une feuille donne lieu à une affectation qui nous permet de couper toutes les branches de l’arbre qui correspondent à une zone plus petite. Il se trouve que les zones sont de plus en plus petites lorsqu’on descend dans l’arbre et que les plus petites zones sont les plus nombreuses.

Même si on a une quantité exponentielle de nœuds à visiter, chaque découverte d’une feuille permet d’économiser une quantité exponentielle de visites.

Après l’analyse de cet algorithme par un professionnel (merci à Paul Zimmerman de l’équipe Algo de l’INRIA), la complexité a été évaluée à n log(n). C’est de très loin meilleur que toutes les autres solutions proposées. Toutes les propositions pour améliorer le programme qui passent par un prétraitement comme un tri ou un hachage des points sont à proscrire si le traitement est plus coûteux que le programme lui-même…

Nous l’avons testé sur des tableaux contenant 1 000 000 de cases noires générées aléatoirement. Le programme faisait en moyenne 200 000 000 d’appels à la fonction appartient qui fait les comparaisons. C’est un comportement typique de la complexité n log(n). Cela veut dire un calcul effectué en dix minutes au lieu de… jamais : 4^1 000 000 a plus de chiffres qu’il n’y a d’atomes dans l’univers.

4.1.4.2.4 Distance entre deux mots

Pour réaliser ce type d’optimisation, il n’est pas nécessaire d’avoir recours à un effet de bord. On peut parfois de manière lisible, comme nous allons le voir dans l’exemple qui suit, avoir recours à des valeurs de contrôle passées en paramètre à nos fonctions.

Définissons la distance entre deux mots comme étant la longueur du plus court chemin entre les deux en utilisant les transformations suivantes :

l’insertion d’une lettre coûte 1
la suppression d’une lettre coûte 1
la substitution d’un lettre à une autre coûte 1

C’est une distance car :

d(mot1,mot2)=0 Û mot1=mot2
d(mot1,mot2)=d(mot2,mot1)
d(mot1,mot2)+d(mot2,mot3)≥d(mot1,mot3)

Seule la dernière affirmation n’est pas triviale, mais il ne me semble pas nécessaire de la démontrer, car il est facile de s’en persuader.

Tentons de décrire l’algorithme de calcul.

Pour trouver une base à notre récurrence, il nous suffit de décrire la distance entre le mot vide et un autre mot quelconque. C’est la longueur de l’autre mot (qui correspond à l’insertion successive de tous les caractères de l’autre mot).
Si les mots ne sont pas vides :
- Si les deux premières lettres sont les mêmes, la distance est égale à la distance des deux mots amputés de leur première lettre. Par exemple, d(plif,plouf)=d(lif,louf).
- Sinon, il existe trois chemins possibles, qui sont l’insertion de la première lettre de mot1, la suppression de cette lettre ou la substitution de la première lettre de mot2 à la première lettre de mot1. Nous évaluerons la distance dans les trois cas envisagés et nous retiendrons la plus courte.

Programmons ces clauses en Lelisp, en supposant que les mots sont représentés par des listes. Il serait très facile de le retranscrire pour qu’il traite des chaînes de caractères, mais lisp signifie List Processing et c’est donc un langage particulièrement adapté à ce genre de représentations.

(de distance (mot1 mot2)
    (cond ((vide mot1) (length mot2))
          ((vide mot2) (length mot1))
          ((eq (tete mot1) (tete mot2))
           (distance (suite mot1) (suite mot2)))
          (t
           (+ 1
              (min (distance (suite mot1) mot2)
                   (distance mot1 (suite mot2))
                   (distance (suite mot1)
                             (suite mot2)))))))

Exemple 4.1.4.3 distance entre deux mots (Lelisp)

Comme pour l’exemple du plus grand rectangle blanc (Exemple 4.1.4.2), nous sommes face à un algorithme de complexité exponentielle, ici 3ⁿ. Ce qui veut dire que pour des mots de longueur non négligeable, le calcul va prendre un temps prohibitif. Ce n’est certainement pas avec ce genre d’idée que nous trouverons le mot le plus proche dans un dictionnaire.

Pourtant, toutes les suppositions ne sont pas nécessaires et chaque fois que nous avons calculé la longueur d’un chemin, comme lorsque nous atteignons une feuille de l’arbre d’évaluation pour le rectangle, nous pouvons couper un grand nombre de calculs.

Nous allons maintenir à jour deux bornes pour la valeur de notre distance. A tout moment du calcul, si on a déjà effectué q transformations, la longueur de ce chemin est au moins de q. Si on a déjà trouvé un chemin plus court, on peut abandonner le calcul. D’autre part, nous connaissons déjà un chemin universel entre deux mots : nous substituons les lettres les une après les autres jusqu’à la fin du mot le plus court, puis nous insérons ou supprimons les dernières lettres du mot le plus long. Ce qui nous donne une distance égale à la longueur du mot le plus long^⁴⁶.

Utilisons ces bornes dans l’exemple suivant :

int distance(liste mot1,liste mot2,
             int resultat,int maximum) {
  if (vide(mot1))
    return resultat+longueur(mot2);
  else if (vide(mot2))
    return resultat+longueur(mot1);
  else if (resultat>=maximum)
    return resultat;
  else if (tete(mot1)==tete(mot2))
    return distance(suite(mot1),suite(mot2),
                    resultat,maximum-1);
  else {
    int d1,d2,d3;
    d1=distance(suite(mot1),suite(mot2),
                resultat+1,maximum);
    if (d1==resultat+1)
      return d1;
    d2=distance(suite(mot1),mot2,
                resultat+1,d1);
    if (d2==resultat+1)
      return d2;
    d3=distance(mot1,suite(mot2),
                resultat+1,min(d1,d2));
    return min3(d1,d2,d3);
  }
}

L’appel initial sera :

distance(mot1,mot2,0,max(longueur(mot1),
longueur(mot2)));

Exemple 4.1.4.4 distance optimisée (C)

C’est très similaire à l’exemple du plus grand rectangle blanc. La seule différence étant dans l’emploi des paramètres plutôt que l’effet de bord sur la variable surfaceMaximale.

4.1.4.2.5 Optimisation αβ dans l’algorithme Min Max

L’algorithme Min Max sert à évaluer des stratégies pour permettre à un ordinateur de jouer contre un humain à des jeux vérifiant certaines conditions : en particulier, une perte pour un des joueurs correspond à un gain équivalent pour l’autre (zero-sum).

Les échecs, les dames, le Go rentrent dans cette catégorie et sont d’excellents exemples de ces jeux dans le sens où on a beaucoup créé de programmes pour y jouer, mais que l’être humain garde encore ses chances.

Pour une recherche à un niveau b de profondeur sur une largeur a, il s’agit de sélectionner les a meilleurs coup a priori, puis pour chacun de ces coups, imaginer les a meilleures réponses possibles, puis encore jusqu’à une profondeur b. Si vous comptez bien, vous arrivez à a^b suppositions de partie avec à chaque étape, une évaluation de toutes les possibilités pour sélectionner les a meilleures.

Il faut ensuite remonter dans l’arbre d’évaluation en notant chaque coup de manière inversement proportionnelle^⁴⁷ à la meilleure des réponses envisagées. Un coup est bon si la meilleure réponse est mauvaise.

Une fois de plus nous sommes face à un algorithme de complexité exponentielle. La célèbre optimisation des coupes α et β est exactement la même que celle que nous venons de voir sur la distance : à chaque niveau, nous maintenons à jour un paramètre correspondant à la meilleure réponse trouvée pour l’instant et un paramètre pour la note maximale possible.

Chaque fois que nous envisageons un calcul, il suffit que nous ayons trouvé une possibilité de réponse suffisamment bonne pour qu’on abandonne l’ensemble du coup courant.

4.1.4.3 Violents effets de bord

Pour l’instant, nous avons touché à l’arbre d’évaluation par des moyens tout à fait corrects. Les coupures se font avant d’entrer dans les sous arbres dont l’évaluation est inutile. Nous ne détruisons jamais aucune information.

Maintenant, lorsque nous découvrons que le calcul en cours est totalement obsolète et qu’un choix que nous avons fait au départ est mauvais, le problème est légèrement différent. On peut de nouveau utiliser des artifices de codage avec une série d’échappatoires. Cela nous demande de vérifier à chaque étape et de prévoir un retour anticipé.

Cela fait en général beaucoup de code et surtout, il y a du code en dehors des endroits pertinents : l’endroit où est détecté le problème et l’endroit où on a fait le mauvais choix.

Lorsqu’au fin fond du programme, on décide que tout ce qui a été calculé depuis un instant t est inutile, il en fait très difficile d’y retourner directement sans repasser par toutes les étapes intermédiaires.

Certains langages évolués proposent des structures permettant d’une part, de signaler un problème à un niveau et de remonter dans l’évaluation, et d’autre part de rattraper ses échappements ailleurs dans la pile d’évaluation.

Il s’agit des exceptions. On peut les gérer en Modula2, en Ada et surtout en Java.

On peut envisager, dans ces langages, d’utiliser le mécanisme des exceptions pour gérer ce type d’intervention. C’est très puissant et avec un peu de discipline, cela reste très lisible.

Dans les langages Lelisp et C, de beaucoup plus bas niveau, il existe les moyens d’effectuer ces effets de bord sur la pile d’évaluation :

en Lelisp, on marque un niveau dans la pile avec la fonction tag. Par la suite, on peut vidanger la pile jusqu’au tag avec la fonction exit qui a le bon goût de nous transmettre son argument comme valeur de retour pour le tag. (Voir aussi la fonction unexit). Ces fonctions de manipulation de la pile d’évaluation m’ont entre autres servies à réaliser l’évaluation intelligente des fonctions récursive terminales cf. Cas des fonctions récursives terminales7.2.1.
en C, les structures prévues sont setjmpbuf et longjmp qui sont d’un emploi particulièrement sportif. Ce sont les fonctions qui servent pour implémenter le multitâche d’UNIX. On crée plusieurs piles d’évaluation et on saute de l’une à l’autre avec un longjmp.

4.2 L’optimisation de code

Ce niveau d’optimisation est parfois réalisé manuellement. Ce que je déconseille vivement pour plusieurs raisons. Le code retouché pour optimisation perd de sa lisibilité. Les optimisations sont souvent liées à un certain type de machine, on perd donc de la portabilité. Et surtout, on va peut-être interdire au compilateur (dont un des rôles est d’optimiser le code pour la machine cible spécifique que vous utilisez) de réaliser certaines optimisations de bas niveau. Bref, il y a plus à perdre qu’à gagner.

Par contre, on peut tenter de présenter des expressions que le compilateur saura facilement évaluer de manière optimale. Voici ce qu’on peut faire sans risque : la dérécursivation.

Une fois bien compris le mécanisme d’une fonction récursive particulière, il peut-être utile de la transformer en boucle itérative, pour économiser le temps et la place mémoire nécessaire à l’empilement de tous les appels, puis le temps de la destruction de tous les environnements locaux.

4.2.1 Cas des fonctions récursives terminales

Dans les langages modernes ainsi que dans Lelisp qui est dédié au récursif et dans le C depuis 1993 avec Watcom et gcc, il est prévu d’évaluer une large classe de fonctions récursive de manière itérative et efficace. Il s’agit des fonctions récursives terminales, dont nous parlions précédemment.

Une fonction est dite récursive terminale si tous les calculs qui la concernent sont finis lors de l’appel récursif. Ce qui signifie qu’aucun calcul n’est mis en suspens lors de l’appel. Disons pour simplifier que les return de la fonction contiennent l’appel récursif au premier niveau.

Dans la fonction f, cet appel récursif est terminal :

return f(e,suite(l))

Ceux-ci ne le sont pas :

return cons(a,f(b))

return f(a) + 1

Dans le dernier cas, il s’agit de rendre la somme, donc le « + 1 » reste en suspens. On ne peut pas évaluer ces fonctions récursive non terminales de manière itérative naturellement parce qu’il faut bien effectuer ces opérations en suspens pendant la remontée.

Voyons comment on transforme une fonction récursive en récursive terminale, puis nous en ferons des boucles itératives (à titre de curiosité, car c’est automatique dans les langages que nous avons cités).

Première phase, on essaie de faire tous les calculs au fur et à mesure. Une bonne technique : passer les résultats intermédiaires en paramètre d’une fonction auxiliaire. Regardons l’exemple de la longueur d’une liste.

function longueur(l:liste):integer;
begin
  if vide(l) then
    return(0)
  else
    return(1 + longueur(suite(l)))
end;

Exemple 4.2.1 7.2.1.1 longeur non terminale (Pascal)

Rajoutons un paramètre accumulateur qui servira à effectuer les additions au fur et à mesure.

function longueur(l:liste):integer;
  function longueur_aux(l:liste;
                        resultat:integer
                       ):integer;
  begin
    if vide(l) then
      return(resultat)
    else
      return(longueur_aux(suite(l),resultat+1)
  end;
begin
  return(longueur_aux(l,0))
end;

Exemple 4.2.1.2 longueur récursive terminale (Pascal)

Le calcul est effectué dès l’appel et il ne reste aucun calcul en suspens. Pourtant, quelque chose a changé dramatiquement. Nous calculons dans l’ordre inverse. Comme l’addition est commutative, cela ne pose ici aucun problème, mais dans le cas de la concaténation, les éléments doivent être ajoutés dans l’ordre. Si on se contente de prendre la fonction append et d’effectuer le calcul des cons au fur et à mesure, on obtient le code de la fonction reverse-aux. Il est nécessaire d’inverser l’argument initial qu’on lui passe :

(de append (l1 l2)
(reverse-aux (reverse l1) l2))

Exemple 4.2.1.3 version récursive terminale de append (Lelisp)

Avec un langage comme Pascal, il sera nécessaire d’aller ensuite jusqu’à l’étape itérative :

function longueur(l:liste):integer;
var
  resultat:integer;
begin
  resultat:=0;
  while not vide(l) do
    begin
      l:=suite(l);
      resultat:=resultat+1
    end;
  return(resultat)
end;

Exemple 4.2.1.4 longueur version itérative (Pascal)

Cela semble plus simple à certaines personnes, mais c’est aussi plus dangereux. Ici, les instructions de départ et les conditions d’arrivée sont simples à programmer, mais ce n’est pas toujours le cas.

4.2.2 Autres cas : les mains dans le cambouis

Certaines fonctions ne se prêtent pas du tout au parcours itératifs. Tout ce qui est parcours d’arbre, tour de Hanoi ou fonction dans laquelle il y a des combinaisons d’appels récursifs, est de nature récursive et ne devrait pas être écrit en itératif. Pourtant, on peut sensiblement améliorer les performances d’un programme en jonglant avec l’interprétation et en gérant nous même la pile d’évaluation de manière simplifiée.

4.2.2.1 Le parcours d’arbre

Nous allons maintenant toucher le fond de la machine. Mettez votre combinaison de mécanicien et vos gants de jardinage. Notre machine ne connaît pas le récursif. En réalité, elle gère une pile d’évaluation avec des goto, des push et des pop.

La légende veut toujours que les fonctions récursives soient moins efficaces que leur version itérative. Cela vient du fait que le compilateur ne sait pas toujours gérer la récursivité de la manière la plus efficace. La zone mémoire réservée à la pile est parfois trop petite. D’autre part le compilateur y stocke toutes les valeurs qui censée pouvoir servir, en l’occurrence une sauvegarde complète de l’environnement local. C’est là que nous allons pouvoir gagner.

Nous pouvons écrire nous-même la gestion de l’évaluation en allouant nous même la pile, garantissant ainsi qu’elle ne soit pas limitée en taille et qu’elle ne contienne que les informations utiles.

Prenons un exemple d’évaluation particulièrement adapté au récursif : le parcours postfixe d’arbre binaire. Nous créons une pile dans laquelle nous simulerons les appels récursifs et le traitement du nœud.

Voici d’abord la version d’origine :

procedure postfixe(a:arbre);
begin
  if not vide (a) then
    begin
      postfixe(fils_gauche(a));
      postfixe(fils_droit(a));
      traitement(tete_arbre(a));
    end
end;

Exemple 4.2.2.1 parcours d’arbre postfixe récursif (Pascal)

C’est élégant et simple. Ca me fait mal au cœur de le transformer, mais allons-y ! Nous avons deux types d’instructions à empiler : les appels à postfixe et les appels à traitement. Nous devons donc les différencier avec un champ booléen traite par exemple. pile est une liste d’element manipulée avec empile qui rajoute l’element et depile qui l’enlève tout en rendant le sommet.

type
  element=record
    arbre:arbre;
    traite:boolean;
  end;
var
  p:pile;
procedure postfixe(a:arbre);
var
  sommet:element;
begin
  p:=pile_vide;
  empile(a,false);
  while not vide(p) do
  begin
    sommet:=depile();
    if sommet.traite then
      traitement(tete_arbre(sommet.arbre))
    else
      begin
        empile(sommet.arbre,true);
        empile(fils_gauche(sommet.arbre),false);
        empile(fils_droit(sommet.arbre),false)
      end
  end
end;

Exemple 4.2.2.2 parcours postfixe en itératif (Pascal)

Notez au passage que nous empilons dans l’ordre inverse de l’évaluation à cause du comportement LIFO.

4.2.2.2 Retour sur le plus grand rectangle blanc

L’évaluation récursive de la fonction de recherche (Exemple 4.1.4.2) peut aussi être transformée en une boucle while.

Il suffit de simuler le comportement de la fonction récursive :

var
  p:pile;{une pile de zone}
function recherche():integer;
var
  z:zone;
  surface_maximale:integer;
  case:point;
begin
  p:=pile_vide;
  empile(zone(1,T,1,T));
  surface_maximale:=0;
  while not vide(p) do
  begin
    z:=depile();
    if surface(z)>surface_maximale then
      begin
        case:=trouve_une_case(z);
        if case=pas_trouve then
          surface_maximale:=surface(z)
        else
        begin
          empile(zone(case.x+1,z.x1,z.y0,z.y1));
          empile(zone(z.x0,case.x-1,z.y0,z.y1));
          empile(zone(z.x0,z.x1,case.y+1,z.y1));
          empile(zone(z.x0,z.x1,z.y0,case.y-1));
        end
      end
  end
end;

Exemple 4.2.2.3 rectangle blanc itératif (Pascal)

On empile de nouveau les quatre appels récursifs afin de les voir traiter. En y réfléchissant bien, on s’aperçoit que l’ordre dans lequel on met les zones dans le pile n’est pas du tout important et qu’on pourrait à n’importe quel instant le changer.

Que se passerait-il si on remplaçait notre pile d’évaluation par une file d’attente ? Notre arbre d’évaluation serait parcouru par étage : on finirait de tester les quatre premières zones définies par la première case avant d’aller dans l’ordre faire les 16 zones suivantes puis les 64 de la troisième couche, et nous nous arrêterions d’empiler dès que nous aurions trouvé des solutions maximales… Apparemment, c’est beaucoup plus rapide. Dans la pratique, il nous faut stocker tellement de zones simultanément qu’il faut un tableau de taille gigantesque (les listes chaînées sont prohibées à cause du parcours) qui ne suffit pas pour les très grandes listes de cases noires et la gestion de cette pile qui a une taille exponentielle nous coûte plus que le calcul lui-même.

Restons en là ! La file d’attente d’évaluation, c’est une très bonne idée, mais pas dans ce cas précis. Tant pis.

4.3 La complexité

Malheureusement, nous ne possédons pas tous les outils nécessaires à l’étude de la complexité. L’utilisation des séries entières dans l’analyse combinatoire n’est enseignée qu’à une poignée de personnes. De toute façon, il n’est pas nécessaire d’être un grand spécialiste^⁴⁸ pour pouvoir estimer la complexité apparente des programmes que nous écrivons ici.

De plus, il est vital de distinguer la complexité du pire des cas, la complexité moyenne et la complexité pratique. Les trois concepts sont complètement différents mais on les confond très souvent.

Nous découvrons parfois avec surprise qu’un algorithme exponentiel en la taille des données se révèle quasi polynomial dans la pratique. A l’inverse, on opte pour l’algorithme de tri rapide pour sa complexité optimale, alors qu’on trie de nombreuses listes de faible taille. C’est peut-être un mauvais choix.

Parfois, à l’aide de quelques heuristiques adaptées ou tout simplement parce que le caractère exponentiel de l’algorithme est limité à des données aléatoires ou des cas d’école, il est possible de résoudre le problème en temps linéaire.

De manière générale, je conseillerais de tenter d’évaluer la complexité moyenne éventuellement, mais de toujours confirmer par la pratique à l’aide d’un prototype.

4.3.1 En temps et en taille

Quand on parle de complexité, on essaie d’évaluer le temps et l’espace mémoire nécessaire à un calcul particulier. Cela peut véritablement être crucial. Parlons par exemple de la décomposition en facteurs premiers des grands nombres. Ce sont des calculs importants car la plupart des systèmes de sécurité reposent sur le fait qu’il faut un temps trop long pour réaliser la fracture d’un nombre de 200 chiffres.

Ces calculs sont très longs. Le problème est réputé NP complet. Ce qui signifie en clair que l’on dispose d’algorithmes exponentiels améliorés par des heuristiques polynomiales plus ou moins efficaces.

Comme il s’agit de la base des programmes de cryptologie, c’est souvent couvert par le secret militaire et c’est aussi très bien payé… Le seul problème qui nous concerne ici, c’est le fait que notre programme va tourner pendant 2 ans sur une machine très coûteuse.

On ne peut pas lancer une évaluation de ce prix là pour découvrir au bout d’un an que le programme échoue par manque d’espace mémoire ni découvrir qu’il ne faut pas 2 ans, mais 20 !

D’où la nécessité de pouvoir estimer correctement la durée et l’espace nécessaires à un calcul.

D’autre part, ces deux données sont liées à de nombreux facteurs et souvent, les économies sur l’un se font au détriment de l’autre. Il va donc nous falloir faire des compromis.

4.3.2 Réduire l’ordre de grandeur de la complexité

On ne cherche pas gratuitement à améliorer les performances d’un programme. L’expérience antérieur ou la réflexion nous demandent parfois d’optimiser a priori un traitement ou un autre, mais le véritable moteur de ce besoin est en général l’expérience pratique née de l’utilisation du prototype.

Il faut parfois savoir ignorer l’apparente complexité théorique pour pouvoir mieux la chiffrer dans la pratique : si on doit traiter un million de données, on mesure le temps de réponse pour une donnée puis pour 10, 100 et 1000 par exemple et on tente d’extrapoler pour le cas pratique.

Ce n’est qu’après l’analyse pratique que l’on peut isoler les parties du programme qui sont véritablement coûteuses et pour lesquelles une optimisation s’impose.

4.3.2.1 Est-ce toujours utile ?

Si je pose cette question, c’est précisément pour insister sur le fait que ça ne l’est pas. Je proposais souvent la solution simple (Exemple 4.1.4.1) à mes étudiants qui trouvait que l’algorithme était trop naïf. Le problème complet que nous avions à résoudre était celui de trouver une expression pour les combinaisons de 1000 éléments dans 500 places.

Evidemment, comme il s’agit d’un nombre beaucoup trop grand pour être représenté avec les entiers de la machine, nous avons choisi (cf. Exemple 6.2.1.1) de représenter les nombres par leur décomposition première ou, plus concrètement par la liste des puissances des facteurs premiers de leur décomposition.

D’où la recherche des nombres premiers vue précédemment. La solution simple en question repose sur la certitude que l’on a sous la main, tous les nombres premiers inférieurs à celui qu’on cherche.

Le programme cherche les nombres premiers en avançant de 1 en 1. Tout programmeur, même sans avoir de grandes connaissances mathématiques, s’imagine faire une grande optimisation en le faisant avancer de 2 en 2. Ce qui est possible à partir de la deuxième étape, car les nombres premiers supérieurs à 2 sont tous impairs. Evidemment, il est nécessaire de régler ces petits détails d’initialisation et le code double de volume.

Il nous semble évident que, comme nous testons deux fois moins de nombres, nous allons calculer deux fois plus vite.

C’est doublement faux : d’une part les nombres paires sont éliminés immédiatement car 2 est le premier candidat à la division et d’autre part, le programme passe très peu de temps dans la recherche de nombres premiers.

L’effet de l’optimisation est nul !

Pour montrer de plus que l’optimisation de ce calcul n’est pas nécessaire, je leur propose souvent très lâchement de programmer le crible d’Euclide^⁴⁹. Le programme croît encore de cinquante lignes et le temps de réponse ne diminue pas (il va même jusqu’à augmenter pour certains).

La recherche des nombres premiers représente 1% du temps d’exécution et donc, toute optimisation est parfaitement inutile.

Par contre, il est immédiatement rentable de transformer notre multiplication de listes en fonction récursive terminale. Cela élimine le problème de dépassement de taille de la pile d’évaluation et cela change l’ordre de grandeur du temps d’évaluation.

4.3.2.2 A quel prix ?

Voilà la bonne question ! Avant de se lancer dans une « optimisation », il faut donc connaître par la pratique la complexité d’une opération et l’importance de celle-ci par rapport au reste du calcul. Il s’agit de savoir ce qu’il y a à gagner. Il faut comparer cela au prix de l’optimisation : gagner sur un plan nous fait perdre sur un autre : les mémofonctions par exemple gagnent du temps en perdant de la place. D’autres optimisations nous coûterons du temps de développement ou pire, de la fiabilité. Le programme devient plus rapide, mais produit des erreurs de temps en temps.

Là encore, connaître la nature du calcul est utile : si le calcul est souvent répété avec les mêmes valeurs, une mémofonction est la bienvenue, mais dans le cas contraire, elle coûte de la place pour un gain négligeable. Dans le cas de nos combinaisons (cf. Exemple 6.2.1.2), pour avoir une expression du factoriel de 30 000, il n’était pas possible de mémoriser toutes les valeurs intermédiaires. Il fallait faire un compromis (n’en stocker qu’un sur 100 par exemple).

Le plus important aujourd’hui, me semble le coût du développement et de la mise au point. Il faut tenir compte de son niveau de maîtrise de l’optimisation considérée. Comme on dit, « γνωτι σεαυτον », il faut connaître ses limites avant de tenter de les reculer.

5 Quelques grandes familles d’algorithmes

5.1 Rechercher l’information

5.1.1 Rechercher de manière linéaire

5.1.1.1 Dans des listes

Donnons rapidement les fonctions de base du type abstrait liste respectivement en Pascal, en Lelisp et en C^⁵⁰ :

type
  liste=^cellule;
  cellule=record
            elt:element;
            suivant:liste;
          end;
const
  liste_vide=nil;

function cons(e:element;l:liste):liste;
var
  nouvelle:liste;
begin
  new(nouvelle);
  nouvelle^.elt:=e;
  nouvelle^.suivant:=l;
  return(nouvelle)
end;

function suite(l:liste):liste;
begin
  return(l^.suivant)
end;

function tete(l:liste):element;
begin
  return(l^.elt)
end;

function vide(l:liste):boolean;
begin
  return(l=liste_vide)
end;

Exemple 5.1.1.1 listes (Pascal)

Nous ne décrivons ici que la version des listes chaînées avec des pointeurs et des cellules.

(setq liste_vide ())
;;cons existe deja sous ce nom

;; avec des macros   ;  avec des fonctions
(dmd suite (l)       ;  (de suite (l)
  `(cdr ,l))         ;    (cdr l))
(dmd tete (l)        ;  (de tete (l)
  `(car ,l))         ;    (car l))
(dmd vide (l)        ;  (de vide (l)
  `(null ,l))        ;    (null l))

Exemple 5.1.1.2 listes (Lelisp)

Notez que le type de base du Lisp étant la liste, toutes les fonctions de base du traitement des listes existent déjà. J’utilise donc des macros pour substituer les appels aux fonctions de bases aux opérations du type abstrait.

typedef struct cellule_liste {
          element elt;
          struct cellule_liste*suivant;
        }*t_liste;
static
  liste_vide=(t_liste)0;
t_liste cons(element e, t_liste l)
{
  t_liste nouvelle;
  nouvelle=(t_liste)malloc(sizeof(nouvelle*));
  nouvelle->elt=e;
  nouvelle->suivant=l;
  return(nouvelle);
}
t_liste suite(t_liste l)
{
  return(l->suivant);
}
element tete(t_liste l)
{
  return(l->elt);
}
int vide(t_liste l)
{
  return(l==liste_vide);
}

Exemple 5.1.1.3 listes (C)

Voyons donc maintenant la recherche linéaire dans ces listes chaînées :

function appartient(e:element;
                    l:liste):boolean;
begin
  if vide(l) then
    return(false)
  else
    if e=tete(l) then
      return(true)
    else
      return(appartient(e,suite(l)))
end;

Exemple 5.1.1.4 recherche (Pascal)

L’exemple en Pascal suppose le type element muni d’un opérateur de comparaison « = ». Si vous manipulez une structure complexe (de type record) dans un Pascal standard, il faudra écrire une fonction de comparaison meme_element et remplacer les expressions a=b par des expressions meme_element(a,b).

Notez qu’on pourrait aussi écrire la valeur de retour en une seule instruction :

begin
return(not vide(l) and
(e=tete(l) or appartient(e,suite(l)))
end;

C’est exactement équivalent. Selon l’habitude, on peut préférer la deuxième pour sa concision ou la première pour son côté explicite.

Voici maintenant la version Lelisp :

(de appartient (e l)
  (cond ((vide l) ())
        ((eq e (tete l)) l)
        (t (appartient e (suite l)))))

Exemple 5.1.1.5 recherche (Lelisp)

Ceci pourrait aussi s’écrire :

(de appartient (e l)
  (and l
       (or (eq e (tete l))
           (appartient e (suite l)))))

C’est la définition de la fonction memq et la première version présente la particularité de rendre une information plus riche : il y a le morphisme de l’ensemble des objets Lisp vers l’algèbre de Boole avec FAUX=nil (noté « () ») et VRAI=toutes les autres valeurs. (Par défaut, on utilise t.) Lorsque l’élément est dans la liste, on rend la place de sa première occurrence^⁵¹. C’est l’information la plus riche possible pour cet algorithme. On peut tout déduire de cette position, aussi bien l’information booléenne correspondant à sa présence dans la liste (on utilise (appartient e l) en tant que booléen) que le nombre d’occurrences (Il suffit de rappeler appartient sur le reste jusqu’à ce qu’il rende ()) ou même la liste des positions des occurrences...

int appartient(element e,liste *l)
{
  if (vide(l))
    return(0);
  else
    if (e==(tete(l))
      return(1);
    else
      return(appartient(e,suite(l)));
}

Exemple 5.1.1.6 recherche (C)

C’est quasiment mot pour mot la version Pascal. La seule particularité vient de l’utilisation explicite des entiers pour représenter les booléens. En C, le morphisme de l’algèbre de Boole sur les données fait correspondre FAUX à toute donnée composée de bit 0 et VRAI à toute autre donnée.

Une fois encore, il serait inutile de donner une version de la recherche linéaire en Java, car la classe Vector est munie de toutes les opérations de recherche dont on peut rêver et il n’est en aucun cas nécessaire de réinventer.

L’ensemble de ces algorithmes de recherche nécessite un parcours complet de la liste avant de pouvoir déterminer la non appartenance d’un élément. Par contre, ils sont économiques à la création^⁵².

5.1.1.2 Dans des listes triées

Si vous disposez d’une relation d’ordre total sur vos éléments, si la recherche est un point coûteux de votre programme et si la construction peut être négligée (par exemple si elle est faite une fois pour toute alors qu’il sera fait beaucoup de recherches), il peut être intéressant de perdre du temps à la création pour l’économiser lors du traitement.

On organise la liste de manière croissante, et alors pour la recherche on pourra déterminer l’appartenance d’un élément à une liste sans parcourir l’ensemble de la liste. On va donc manipuler des listes triées.

Sorte : Liste_triée

Utilise : (Elément, <), Booléen

Opération :

inserer : Elément, Liste_triée ® Liste_triée
rechercher : Elément, Liste_triée ® Booléen

Et éventuellement

fusion : Liste_triée, Liste_triée ® Liste_triée

Type abstrait 5.1.1.1 listes triées

Une fois de plus il va falloir choisir entre plusieurs stratégies : si les éléments vous sont donnés au compte goûte (saisie de l’utilisateur par exemple), il faudra choisir de trier les éléments à l’insertion.

function inserer(e:element;l:liste):liste;
begin
  if (vide(l)) or (e<tete(l)) then
    return(cons(e,l))
  else
    return(cons(tete(l),
                inserer(e,suite(l)))) end;

Exemple 5.1.1.7 insertion dans une liste triée (Pascal)

Notez que nous utilisons directement le type liste pour représenter les listes triées. Ce sont les propriétés qui changent et la structure reste physiquement la même.

(de inserer (e l)
  (if (or (vide l)
          (< e (tete l)))
      (cons e l)
      (cons (tete l)
            (inserer e (suite l)))))

Exemple 5.1.1.8 insertion dans une liste triée (Lelisp)

Il est possible d’améliorer sensiblement l’efficacité de ces fonctions en réalisant une insertion physique dans le deuxième argument. Dans l’exemple suivant en C, nous passons la liste par référence et nous réalisons un effet de bord qui nous permet de ne pas reconstruire le début de la liste. Ce n’est possible que si nous n’avons plus besoin de l’ancienne version de la liste.

void insertion (element e,t_liste*pl)
{
  if ((vide(*pl))||(e<tete(*pl)))
    *pl=cons(e,*pl);
  else
    insertion(e,&((*pl)->suiv));
}

Exemple 5.1.1.9 insertion physique dans une liste triée (C)

Ceci permettra d’économiser un appel au gestionnaire de mémoire. Il faudra en conséquence l’appeler avec « insertion(e,&l); ». Notez au passage qu’il n’est pas nécessaire de tenir compte des cas particuliers de l’insertion en tête ou en queue de liste, mais, je le répète, il y a une modification physique du contenu de la liste. C’est d’un emploi quelque peu barbare, mais pour les amis du C, c’est très joli^⁵³ !

Par contre, si les éléments vous arrivent d’un seul bloc dans une liste non triée, le choix naturel sera un tri fusion par exemple (c’est un excellent rapport qualité/prix^⁵⁴), plutôt que le tri par insertion. La définition de rg_pair et rg_impair est dans l’Exemple 3.2.3.4.

function tri_fusion(l:liste):liste;
begin
  if vide(l) or vide(suite(l)) then
    return(l)
  else
    return(fusion(tri_fusion(rg_pair(l)),
                  tri_fusion(rg_impair(l))))
end;

Notons au passage que la base de notre récurrence suppose qu’une liste à un élément est triée^⁵⁵. Sinon, le tri fusion scinde une liste à un élément en une liste à un élément et la liste vide, d’où une boucle infinie.

Exemple 5.1.1 8.1.1.10 tri fusion (Pascal)

Ce qui utilise la fonction de fusion de deux listes triées que l’on programmer ainsi :

function fusion(l1,l2:liste):liste;
begin
  if vide(l1) then
    return(l2)
  else
    if vide(l2) then
      return(l1)
    else
      if tete(l1)<tete(l2) then
        return(cons(tete(l1),
               fusion(suite(l1),l2)))
      else
        return(cons(tete(l2),
               fusion(l1,suite(l2))))
end;

Exemple 5.1.1.11 fusion de deux listes triées (Pascal)

C’est une version purement fonctionnelle sans effet de bord. Comme les deux anciennes listes ne sont plus utiles, on peut sensiblement améliorer en utilisant une version procédurale qui reconstruit le chaînage sans faire appel au constructeur. Le nombre de cellules ne changeant pas, c’est possible. En voici une version possible en C :

t_liste tri_fusion(t_liste l) {
  if(vide(l)||vide(suite(l))) {
    return l;
  } else {
    return fusion(&tri_fusion(rg_pair(l)),
                  &tri_fusion(rg_impair(l)));
  }
}
t_liste fusion(t_liste*pl1,t_liste*pl2) {
  if(vide(*pl1)) {
    return *pl2;
  } else if(vide(*pl2)) {
    return *pl1;
  } else if(tete(*pl1)<tete(*pl2)) {
    (*pl1)->suiv=fusion(&suite(*pl1),pl2);
    return *pl1;
  } else {
    (*pl2)->suiv=fusion(pl1,&suite(*pl2));
    return *pl2;
  }
}

Exemple 5.1.1.12 tri fusion physique (C)

Cette fonction est particulièrement « rusée » et utilise la possibilité unique au C de permettre de passer la référence à un résultat de fonction, ce qui est particulièrement sportif, voire d’un emploi très discutable.

La recherche se fait alors grâce au parcours désormais classique de l’insertion.

t_liste rechercher(element e,t_liste l)
{
  if ((vide(l)) || (e<tete(l)))
    return(liste_vide);
  else
    if (e==tete(l)) then
      return(l);
    else
      return(rechercher(e,suite(l));
}

Exemple 5.1.1.13 recherche dans une liste triée (C)

Nous utilisons encore le morphisme avec l’algèbre de Boole : nous rendons une liste en tant que booléen.

La différence avec la recherche dans une liste non triée réside dans l’ajout de || (e<tete(l)) dans la condition de la clause de base. Dans le cas où l’élément recherché ne se trouve pas dans la liste, il est possible donc d’arrêter la recherche dès que l’on trouve un élément supérieur. C’est à peine plus intéressant, mais ce n’est pas la seule utilisation possible du tri.

8.1.1.3Quelques algorithmes de tri, juste pour rire

Voici deux méthodes de tri qui méritent un petit détour.

5.1.1.3.1 Le tri rapide (Quicksort)

Pour le comprendre, il suffit de comprendre le tri fusion et de tenter de diminuer le nombre d’étapes en plaçant un objet directement à sa place à chaque appel.

En voici une version en C pour ne pas changer :

t_liste tri(t_liste l) {
if ((vide(l)))
  return l;
else
  return append(tri(p_ptit(tete(l),
                           suite(l))),
                cons(tete(l),
                     tri(p_grand(tete(l),
                                 suite(l)))));
}

Exemple 5.1.1.14 tri rapide (C)

L’algorithme de base se déroule ainsi : on choisit un élément (ici la tête) qui sera le pivot. On scinde le reste des éléments en deux listes, celle des éléments qui sont plus petit que le pivot et celle de ceux qui sont plus grands. On tri ces deux tas séparément puis on concatène les deux listes résultantes avec le pivot entre les deux.

Il s’agit comme pour le tri fusion d’une stratégie « diviser pour régner ». La complexité est ici meilleure que le n log(n) du tri fusion mais seulement si le pivot est bien choisi. En effet, si la liste est déjà partiellement triée, la scission ne sépare pas en deux tas équivalents et au lieu d’avoir moins de log(n) étapes, on peut se retrouver avec n étapes.

La fragilité de cet algorithme peut être compensée en mélangeant préalablement pour optimiser le tri. Hallucinant, n’est-ce pas ?

5.1.1.3.2 Le tri interclassement monotone

Pour celui-ci, il s’agissait à l’époque ou cette méthode a été conçue, de trier des objets qui étaient représentés physiquement sur une bande magnétique.

Comme pour les fichiers en Pascal, il n’est pas question de revenir en arrière et on ne peut avoir qu’un nombre faible d’endroits où stocker les informations intermédiaires.

On va se débrouiller ici avec trois bandes et une seule variable. Voici le principe.

A chaque étape, on sépare les suites croissantes de la bande d’origine en les copiant alternativement sur la deuxième et sur la troisième bande, puis on fusionne le tout avec l’équivalent de la fonction fusion de l’Exemple 5.1.1.11. Ainsi, la longueur moyenne des sous suites croissantes a tendance à doubler. On s’arrête lorsque la liste est triée (On s’en aperçoit quand toute la première bande est copiée sur la deuxième). L’exemple suivant montre comment utiliser cet algorithme sur une liste. Evidemment il est à utiliser lorsque les données sont sur un fichier à accès séquentiel par exemple.

(de tri (l)
  (tri-aux (tete l)
           (suite l)
           (list (tete l))
           ()))
(de tri-aux (e l l1 l2)
  (cond ((null l)
         (if (null l2)
             l1       ;on a fini
             (tri (fusion (reverse l1)
                          (reverse l2)))))
        ((< e (tete l))
         (tri-aux (tete l)
                  (suite l)
                  (cons (tete l) l1)
                  l2))
        (t     ;on trouve une decroissance
         (tri-aux (tete l)
                  (suite l)
                  (cons (tete l) l2)
                  l1))))

Exemple 5.1.1.15 tri interclassement monotone de liste (Lelisp)

Cette fonction est particulièrement efficace sur des listes déjà partiellement triées comme l’annuaire téléphonique. De plus, nous avons une complexité équivalente au tri fusion, à peine moins bonne que le meilleur des cas de Quicksort.

Déroulons son évaluation sur l’exemple du pire des cas : la liste est dans l’ordre inverse.

Première étape de scission :

(tri (9 8 7 6 5 4 3 2 1 0))
(tri-aux 9 (8 7 6 5 4 3 2 1 0) (9) ())
(tri-aux 8 (7 6 5 4 3 2 1 0) (8) (9))
(tri-aux 7 (6 5 4 3 2 1 0) (7 9) (8))
(tri-aux 6 (5 4 3 2 1 0) (6 8) (7 9))
(tri-aux 5 (4 3 2 1 0) (5 7 9) (6 8))
(tri-aux 4 (3 2 1 0) (4 6 8) (5 7 9))
(tri-aux 3 (2 1 0) (3 5 7 9) (4 6 8))
(tri-aux 2 (1 0) (2 4 6 8) (3 5 7 9))
(tri-aux 1 (0) (1 3 5 7 9) (2 4 6 8))
(tri-aux 0 () (0 2 4 6 8) (1 3 5 7 9))

Ensuite intervient la fusion des listes inversées puis l’étape de scission suivante :

(tri (8 6 4 2 0 9 7 5 3 1))
(tri-aux 8 (6 4 2 0 9 7 5 3 1) (8) ())
(tri-aux 6 (4 2 0 9 7 5 3 1) (6) (8))
(tri-aux 4 (2 0 9 7 5 3 1) (4 8) (6))
(tri-aux 2 (0 9 7 5 3 1) (2 6) (4 8))
(tri-aux 0 (9 7 5 3 1) (0 4 8) (2 6))
(tri-aux 9 (7 5 3 1) (9 0 4 8) (2 6));croissance
(tri-aux 7 (5 3 1) (7 2 6) (9 0 4 8))
(tri-aux 5 (3 1) (5 9 0 4 8) (7 2 6))
(tri-aux 3 (1) (3 7 2 6) (5 9 0 4 8))
(tri-aux 1 () (1 5 9 0 4 8) (3 7 2 6))

Puis

(tri (6 2 7 3 8 4 0 9 5 1))
(tri-aux 6 (2 7 3 8 4 0 9 5 1) (6) ())
(tri-aux 2 (7 3 8 4 0 9 5 1) (2) (6))
(tri-aux 7 (3 8 4 0 9 5 1) (7 2) (6));croissance
(tri-aux 3 (8 4 0 9 5 1) (3 6) (7 2))
(tri-aux 8 (4 0 9 5 1) (8 3 6) (7 2));croissance
(tri-aux 4 (0 9 5 1) (4 7 2) (8 3 6))
(tri-aux 0 (9 5 1) (0 8 3 6) (4 7 2))
(tri-aux 9 (5 1) (9 0 8 3 6) (4 7 2));croissance
(tri-aux 5 (1) (5 4 7 2) (9 0 8 3 6))
(tri-aux 1 () (1 9 0 8 3 6) (5 4 7 2))

Puis la quatrième étape. Notez comme les plus grands chiffres se déplacent vers la droite et les plus petits vers la gauche.

(tri (2 6 3 7 4 5 8 0 9 1))

N’observons plus les étapes intermédiaires, voici la trace des appels de tri.

(tri (2 3 6 4 5 7 0 8 1 9))

(tri (2 3 4 5 6 0 7 1 8 9))

(tri (0 2 3 4 5 6 1 7 8 9))

(tri (0 1 2 3 4 5 6 7 8 9))

Et là on s’arrête. Il nous a fallu huit étapes. C’est un peu meilleur que Quicksort sur le même problème qui demandera 10 étapes. Les étapes nécessitent un traitement de tous les éléments de la liste. Il se trouve que nous avons souvent des listes déjà partiellement triées, mais jamais de listes dans l’ordre inverse (et si c’était le cas, il nous suffirait de l’inverser pour ce tri, ce qui ne servirait à rien pour Quicksort).

5.1.2 La recherche arborescente

Nous nous bornerons pour l’instant aux arbres binaires de recherche, car c’est l’étape la plus nette dans les optimisations dues au choix d’une structure de données. On peut encore améliorer avec des telle que les arbres-2-3, arbres-2-3-4 ou autres arbres bicolores. Mais le coût d’implantation n’est pas toujours inférieur à celui d’une table de hachage bien conçue, qui permettra des calculs bien plus puissants et rapides.

D’ailleurs, ce type n’existe pas à la base en Java, ce qui est un signe manifeste d’inutilité. Mais cela nous donnera l’occasion d’écrire un petit peu de Java, ce que nous n’avons pas fait depuis le chapitre précédent.

5.1.2.1 Les arbres binaires

Comme nous l’avons suggéré, l’idée maîtresse est de rapprocher l’information de la racine. Pour représenter les informations de manière arborescente, il nous faut définir le type abstrait sous-jacent, arbre binaire, avec son constructeur et ses fonctions de manipulation de base.

Sorte : Arbre

Utilise : Elément, Booléen

Opérations :

arbre_vide : ® Arbre
cons_arbre : Elément, Arbre, Arbre ® Arbre
tete_arbre : Arbre ® Elément
fils_gauche : Arbre ® Arbre
fils_droit : Arbre ® Arbre
vide? : Arbre ® Booléen

Préconditions :

tete_arbre(a) n’existe que si non vide?(a)
fils_gauche(a) n’existe que si non vide?(a)
fils_droit(a) n’existe que si non vide?(a)

Axiomes :

" a,b Î Arbre et " E Î Elément

tete_arbre(cons_arbre(e,a,b))=e
fils-gauche(cons_arbre(e,a,b))=a
fils_droit(cons_arbre(e,a,b))=b

Type abstrait 5.1.2.1 les arbres binaires

Le type se manipule sans aucun problème en Lelisp grâce à la structure de base des listes. Les « nœuds » des arbres sont représentés par des listes de trois atomes qui sont respectivement, l’élément, le fils gauche et le fils droit (Notons au passage que la plupart des dialectes de Lisp sont munis d’une structure équivalente aux tableaux nommée vector. Il est alors possible d’avoir un accès encore plus direct à l’information. On peut de plus rajouter un entête qui simulera un typage).

(setq arbre_vide ())
(dmd cons_arbre (elt fgauche fdroit)
  `(list ,elt ,fgauche ,fdroit))
(dmd tete_arbre (arbre)
  `(car ,arbre))
(dmd fils_gauche (arbre)
  `(car (cdr ,arbre)))
(dmd fils_droit (arbre)
  `(car (cdr (cdr ,arbre))))
(dmd vide (arbre)
  `(null ,arbre))

Exemple 5.1.2.1 arbres binaires (Lelisp)

Les macros Lelisp ne sont là que pour masquer l’utilisation directe des fonctions primitives du langage.

Des structures parfaitement équivalentes à base de listes chaînées peuvent être implantées en Pascal et en C, mais nous préfèrerons utiliser des structures spécifiques plus adaptées.

D’abord la version Pascal :

type
  arbre=^cellule;
  cellule=record
            elt:element;
            f_gauche:arbre;
            f_droit:arbre;
          end;
const
  arbre_vide=nil;

function cons_arbre(e:element;g,d:arbre):arbre;
var
  nouveau:arbre;
begin
  new(nouveau);
  nouveau^.elt:=e;
  nouveau^.f_gauche:=g;
  nouveau^.f_droit:=d;
  return(nouveau)
end;

function tete(a:arbre):element;
begin
  return(a^.elt)
end;

function f_gauche(a:arbre):arbre;
begin
  return(a^.f_gauche)
end;

function f_droit(a:arbre):arbre;
begin
  return(a^.f_droit)
end;

function vide(a:arbre):boolean;
begin
  return(a=arbre_vide)
end;

Exemple 5.1.2.2 arbres binaires (Pascal)

Ensuite la version C sensiblement équivalente :

typedef struct cellule_arbre {
  element elt;
  struct cellule_arbre *f_gauche,
                       *f_droit;
}*t_arbre;

static t_arbre arbre_vide=(t_arbre)0;

t_arbre cons_arbre(element e,arbre g,arbre d) {
  t_arbre nouveau;
  nouveau=(t_arbre)malloc(sizeof(nouveau*));
  nouveau->elt=e;
  nouveau->f_gauche=g;
  nouveau->f_droit=d;
  return(nouveau);
}

t_arbre tete(t_arbre a) {
  return(a->elt);
}

t_arbre f_gauche(t_arbre a) {
  return(a->f_gauche);
}

t_arbre f_droit(t_arbre a) {
  return(a->f_droit);
}

int vide(t_arbre a) {
  return(a==arbre_vide);
}

Exemple 5.1.2.3 arbres binaires (C)

public class Arbre {
  public static Arbre arbre_vide=null;
  public Element elt;
  public Arbre gauche;
  public Arbre droit;
  public Arbre(Element elt,
               Arbre gauche,
               Arbre droit) {
    this->elt=elt;
    this->gauche=gauche;
    this->droit=droit;
  }
  public Element tete() {
    return elt;
  }
  public Arbre fils_gauche() {
    return gauche;
  }
  public Arbre fils_droit() {
    return droit;
  }
}

Exemple 5.1.2.4 arbres binaires (Java)

5.1.2.2 Rajoutons la relation d’ordre

Si notre type abstrait Elément est muni d’une relation d’ordre totale, il nous est possible de représenter nos ensembles d’objets avec une sorte de recherche dichotomique intégrée : les arbres binaires de recherche.

Nous allons trier les éléments à l’insertion dans l’arbre de manière moins coûteuse que pour une liste triée. Il faut que nous mettions les éléments de façon à ce que tout ce qu’il y a dans le sous arbre gauche soit inférieur à l’élément de la tête, qui sera lui-même inférieur à tous les éléments du sous arbre droit.

Voyons le type abstrait :

Sorte : ABR (Arbres Binaires de Recherche)

Utilise : (Elément,<), Booléen

Opérations :

insérer : Elément, ABR ® ABR
recherche : Elément, ABR ® Booléen

Axiomes :

" e Î Elément, " a Î ABR recherche(e,inserer(e,a)) est vrai

Type abstrait 5.1.2.2 arbres binaires de recherches (ABR ou AVL)

Voyons comment on peut les programmer sur la base des arbres binaires dans nos langages. Il suffit de rajouter les deux opérations. Ici nous optons pour l’insertion aux feuilles plus simple à expliquer ou à programmer que l’insertion à la racine^⁵⁶.

function insertion(e:element;a:arbre):arbre;
begin
  if vide(a) then
    return cons(e,a,a)
  else if e<tete(a) then
    return cons(tete(a),
                insertion(e,fils_gauche(a)),
                fils_droit(a))
  else
    return cons(tete(a),
                fils_gauche(a),
                insertion(e,fils_droit(a))
end;

function recherche(e:element;a:arbre):boolean;
begin
  if vide(a) then
    return false
  else if e=tete(a) then
    return true
  else if e<tete(a) then
    return recherche(e,fils_gauche(a))
  else
    return recherche(e,fils_droit(a))
end;

Exemple 5.1.2.5 ABR (Pascal)

(de insertion (e a)
    (cond ((null a) (cons_a e a a))
          ((< e (tete a))
           (cons_a (tete a)
                   (insertion e (fils_g a))
                   (fils_d a)))
          (t
           (cons_a (tete a)
                   (fils_g a)
                   (insertion e (fils_d a))))))

(de recherche (e a)
    (cond ((null a) ())
          ((= e (tete a)) t)
          ((< e (tete a))
           (recherche e (fils_g a)))
          (t
           (recherche e (fils_d a)))))

Exemple 5.1.2.6 ABR (Lelisp)

On peut maintenant économiser les opérations de reconstruction de l’arbre si on n’a plus besoin de la version précédente de l’arbre (celle qui ne contient pas l’élément). C’est possible dans tous les langages précédents, mais nous ne nous ne le verrons qu’en Java.

public static Arbre insertion(Element e,
                              Arbre a) {
  if(a.vide()) {
    return new Arbre(e,a,a);
  } else if(e.a.tete) {
    a.gauche=insertion(e,a.gauche);
    return a;
  } else {
    a.droit=insertion(e,a.droit);
    return a;
  }
}

L’insertion se fait en remplaçant directement la référence au fils par l’insertion de l’élément dans ce fils.

public static boolean recherche(Element e,
                                Arbre a) {
  if(a==Arbre.arbre_vide) {
    return false;
  } else if(e==a.tete()) {
    return true;
  } else if(e<a.tete()) {
    return recherche(e,a.gauche);
  } else {
    return recherche(e,a.droit);
  }
}

Exemple 5.1.2.7 ABR avec insertion physique (Java)

5.1.3 Le hachage

Il faut maintenant arriver à manipuler les objets en temps constant. Trouver le moyen d’insérer et de rechercher les éléments considérés dans la structure avec une opération atomique (d’un seul morceau, sans appels récursifs ou boucles).

Si l’ensemble des clés permettant de manipuler ces objets était tout simplement les entiers compris entre 1 et t, il suffirait d’utiliser un tableau de taille t.

Il est possible de se ramener à ce cas trivial.

Imaginons un tableau de la taille nécessaire et une bijection entre l’ensemble E des clés et l’ensemble des indices du tableau. Il est alors possible d’accéder directement aux éléments.

On ne dispose pas toujours d’une bijection mais une injection nous suffirait : il faut qu’un indice différent corresponde à tous les objets que nous manipulons. Si notre fonction n’est pas tout à fait injective, on pourra s’en sortir, par quelques transformations simples (résolution de collisions).

5.1.3.1 Avant de partir

Il n’est pas ici question de cataloguer exhaustivement toutes les méthodes de hachage, les gens intéressés pouvant toujours trouver ce type d’informations dans des livres dont c’est la vocation.

Par contre, l’objectif est de bien cerner l’idée et ce que cela implique.

Notons E, l’ensemble des clés et N l’ensemble des entiers naturels.

5.1.3.2 Une injection de E dans N

Si notre espace mémoire était illimité, on pourrait toujours trouver une injection satisfaisante de E dans l’espace des adresses. Il suffirait d’utiliser le codage de la clé directement comme une adresse. Deux clés différentes ont forcément deux codages différents. Mais le format des adresses est fixe et de petite taille alors que les clés peuvent être vraiment très longues. De plus, la taille des informations à ranger dans la mémoire n’est pas forcément inférieure à la distance entre deux adresses.

On va plutôt imaginer un tableau d’informations repérées par des indices entiers positifs.

L’ensemble des clés est toujours représentable par un ensemble d’entiers. En effet, leur représentation physique dans la mémoire peut toujours être lue comme un entier, en oubliant les limitations de taille.

Par exemple, si les clés sont des chaînes de caractères, on peut toujours les lire en tant qu’entiers. En PASCAL, cela donnerait :

function entier(cle:chaine):integer;
var
  i,res:integer;
begin
  res:=0;
  for i:=1 to length(cle) do
    res:=256*res + ord(cle[i]);
  return(res)
end;

Exemple 5.1.3.1 fausse fonction de hachage (Pascal)

Ce qui va exploser dès que la chaîne de caractères dépasse les quatre caractères (la taille d’un entier). Il nous faut donc revenir dans les limites de notre tableau dont nous noterons la taille T.

5.1.3.3 Une surjection de E sur [0 , T[

Il nous reste alors à faire correspondre ces entiers à des indices du tableau.

Pour que l’attribution de ces indices soit bien répartie (pour tenter d’éviter d’attribuer la même adresse à deux clés), le plus simple est de choisir T premier et d’utiliser le modulo. Ce qui donnerait en Pascal :

type
  indice=[0..t-1];
function hash(cle:chaine):indice;
var
  i,res:integer;
begin
  res:=0;
  for i:=1 to length(cle) do
    res:=(256*res + ord(cle[i]))
         mod t;
  return(res)
end;

Exemple 5.1.3.2 fonction de hachage classique (Pascal)

Pourquoi un nombre premier? Imaginons un instant un cas extrême : T est multiple de 256. Prenons même T=256, le modulo peut-être calculé directement : c’est la valeur du dernier caractère.

Ce qui signifie que deux clés finissant par la même lettre aurait le même code. Les autres lettres n’auraient pas le moindre effet sur le résultat.

Ce qui veut dire en outre que parmi les 256 cases du tableau, seules les 26 lettres de l’alphabet ont une chance de servir. Nous voudrions répartir nos éléments dans tout le tableau.

Nous voulons aussi que toutes les lettres de notre clé aient la même importance. Cela signifie que pour un mot quelconque et un rang quelconque au sein du mot, l’image par notre fonction de hachage de l’ensemble des mots engendrés en mettant n’importe quel caractère dans le mot à ce rang, soit équitablement répartie dans notre tableau. Ce n’est pas très clair ? Expliquons plus concrètement.

Il suffirait d’étudier l’image de la fonction hash sur les ensembles de données suivantes :

aaaa,aaab,aaac,aaad ...
aaaa,aaba,aaca,aada ...
aaaa,abaa,acaa,adaa ...
aaaa,baaa,caaa,daaa ...

Ces images sont des cycles. Un cycle de ce type possède un cardinal qui divise la taille du tableau. Afin que le cycle décrivent obligatoirement la totalité du tableau, il est nécessaire que pgcd(256,T)=1, ce qui est toujours vrai lorsque T est premier.

C’est fini pour les explications compliquées. Revenons donc à notre problème. Nous avons assuré que pour deux clés différentes et un tableau de taille T, nous avons une chance sur T d’avoir la même valeur. C’est bien. Mais que ce passe-t-il si cela arrive quand même ?

5.1.3.4 Boum ! Une collision

Comme nous cherchons à stocker un nombre potentiellement infini d’objets dans une place finie, il y a un côté inévitable à la collision de deux clés. Même avec une fonction de hachage idéale, si nous rangeons n+1 objets, dans n places, il est clair qu’au moins deux clés auront le même indice. C’est ce qu’on appelle une collision.

Nous allons donc utiliser une méthode de résolution des collisions. Si notre fonction de hachage est bonne et si la taille du tableau est suffisamment grande, cela reste un phénomène rare, mais il nous faut bien gérer le problème afin de ne pas perdre de l’information^⁵⁷.

Avant de choisir une fonction de hachage et une méthode résolution des collisions, il faut analyser l’ensemble des clés à ranger dans le tableau. Il faut en déterminer la taille idéale (souvent de manière empirique). Si le tableau est trop petit, on va avoir trop de collisions, s’il est trop grand, on perd de la place.

Voici d’abord deux techniques simples pour résoudre les collisions.

Ce n’est pas exhaustif, mais ce sont deux bons compromis entre l’efficacité et le temps de développement.

Les deux paragraphes suivants exposent une dernière méthode qui me parait pertinente de par sa souplesse.

5.1.3.4.1 Une liste de clefs

Quand la place est limitée, on peut sacrifier un peu de temps d’accès de la manière suivante :

On va utiliser T listes d’éléments, rangées dans les T cases du tableau. Si la fonction de hachage fonctionne de manière optimale pour n éléments, il y aura en moyenne n/T éléments par liste. Ce qui signifie qu’au prix d’une opération de calcul d’indice, nous aurons divisé par T le nombre de comparaisons nécessaires à l’insertion et à la recherche.

Il est alors très facile de régler le compromis place utilisée/temps de calcul : il suffit de régler la taille du tableau.

Le type abstrait correspondant repose sur le type abstrait Liste (Type abstrait 2.2.1.4) ou Liste_triée (Type abstrait 5.1.1.1). On pourrait aussi utiliser les arbres binaires de recherche (Type abstrait 5.1.2.2), mais ce serait bien inutilement compliqué, car n/T est censé valoir moins de 1 (un remplissage à 40% donne de bon résultats).

Sorte : Table_hachage

Utilise : Liste, Elément

Opérations :

insertion : Elément, Table_hachage ® Table_hachage
recherche : Elément, Table_hachage ® Liste

Type abstrait 5.1.3.1 tables de hachage avec chaînage séparé

Notez que l’on va rendre une Liste comme résultat de la recherche dans les Listes.

On utilise alors les fonctions inserer et rechercher déjà programmées pour les listes, listes triées ou arbres selon.

Voici une implémentation rapide en Pascal :

type
  Table_de_hachage=array [0..t-1] of
                    Liste_d_elements;
Var
  Table:Table_de_hachage;
procedure insertion_table(e:Element);
begin
  Table[hash(e.cle)]=insertion_liste(e,
                       Table[hash(e.cle)]);
end;
function recherche_table(c:Cle):Liste_d_element;
begin
  return recherche_liste(c,table[hash(c)]);
end;

Exemple 5.1.3.3 hachage avec chaînage séparé (Pascal)

5.1.3.4.2 Une solution simple, le « linear probing »

Dans ces méthodes, le choix de la taille T influe directement sur le nombre de collisions. Pour une plus grande efficacité, il suffit de sacrifier de la place mémoire en prenant un tableau plus grand.

Dans le cas où l’on peut estimer une borne supérieure au nombre d’objets à stocker et où la place n’est pas cruciale, voici une méthode facile à implanter : le « linear probing ».

Les inconvénients de cette méthode sont donc le gaspillage de la place (la table doit être remplie à 40% au maximum pour être efficace) et le manque de souplesse (si on dépasse cette taille, le programme devient de moins en moins efficace et ne fonctionne carrément pas en cas de dépassement de taille).

t_element table[T];
static t_element inoccupe=(t_element)0;

void insertion(t_element e) {
  int i=hash(e->cle);
  while(table[i]!=inoccupe) {
    i=(i+1)%T;
  }
  table[i]=e;
}
t_element recherche(t_cle c) {
  int i=hash(c);
  while(table[i]!=innocupe &&
        !equal(table[i]->cle,c)) {
    i=(i+1)%T;
  }
  return table[i];
}

Exemple 5.1.3.4 linear probing (C)

Cette méthode présente aussi le désavantage de ne pas permettre facilement la suppression d’un élément de la table. En effet, lorsqu’une série de collisions a eu lieu autour d’un indice, il y a portion du tableau où toutes les cases contiguës sont occupées. Si on venait à en ôter une, il faudrait reconstruire toute la portion en question pour éviter à la table de perdre son intégrité.

5.1.3.4.3 Une famille de tables de tailles croissantes

Je propose une méthode beaucoup plus lourde mais qui permet de traiter le cas général : on a besoin de traiter une quantité inconnue de données qui peuvent arriver à n’importe quel instant.

Nous allons allouer dynamiquement des tables de taille croissante : au départ, nous stockons nos éléments dans un tableau de taille 11 par exemple. Dès la première collision, nous allouons un nouveau tableau de taille 101. Tous les éléments entrant en collision au premier niveau sont donc transférés au niveau 2. De même, si un élément est en collision au niveau 1, puis de nouveau en collision au niveau 2, nous allouerons une nouvelle table au niveau 3 de taille 1001^⁵⁸.

De même pour la recherche, tant que l’on n’a pas trouvé l’élément ou une place inoccupée ou la dernière table (signes du fait que l’élément n’est pas dans la table), on cherche au niveau suivant.

Sachez que cela n’est nécessaire ni en Lelisp, ni en Java.

La fonction de hachage doit alors intégrer la notion de taille variable :

int hash(char*cle,int taille) {
  int res=0,i;
  for(i=0;cle[i];i++) {
    res=(res*256 + cle[i])%taille;
  }
  return res;
}

Exemple 5.1.3.5 fonction de hachage variable (C)

Pour la suite de l’implémentation, nous utiliserons le type Liste avec, comme éléments, des tables.

t_liste ltable=liste_vide;
int[] tailles={11,101,1001,10001,100001};

void inser_aux(t_element e,int niv,t_liste*pl) {
  int indice=hash(e->cle,tailles[niv]);
  if(vide(*pl)) {
    *pl=(t_element*)malloc(tailles[niveau]*
                           sizeof(t_element));
    /* on initialise le tableau tete(*pl) pour
       qu’il contienne inoccupe partout. */
  }
  if(tete(*pl)[indice]==inoccupé)
    tete(*pl)[indice]=e;
  else
    inser_aux(e,niv+1,&suite(*pl));
}

void insertion(t_element e) {
  inser_aux(e,0,&ltable);
}

Exemple 5.1.3.6 liste de tables de tailles croissantes (C)

Nous allouons les tables dynamiquement. C’est-à-dire que l’allocation de la mémoire pour une table se fait lors de sa première utilisation. Dans la pratique, cela signifie que l’ordre de grandeur de la mémoire utilisée est équivalent à celui du nombre d’objets représentés.

5.1.3.5 Tout un univers d’applications possibles

Le hachage se prête à la résolution de nombreux problèmes. Il ne s’agit pas seulement de ranger des informations repérées par des clés.

Par exemple, de nombreux langages proposent des structures de choix multiples avec des branchements directes :

en Pascal : case <expr> of
en C et Java : switch (<expr>)
en Lelisp : (selectq <expr>

Pour brancher l’évaluation sur la suite d’instruction correspondant à la valeur de <expr>, sans faire une série de comparaisons coûteuse, on utilise un hachage adapté.

On peut aussi utiliser le hachage dans la compression de données en représentant chaque mot par son code de hachage (son indice dans le tableau) plutôt que par son expression complète.

Oracle utilise le hachage de la prononciation d’un mot pour proposer toutes les variables pouvant s’approcher d’un mot mal orthographié.

5.2 Reconnaître l’information

Deuxième problème courant en informatique, nous avons besoin de reconnaître de l’information. Parfois, il s’agit de reconnaître une forme dans une image, problème complexe que je ne traiterai pas ici, parfois de trouver un objet spécifique dans une structure.

5.2.1 Parenthèse sur l’unification

Lorsque nous avons besoin de reconnaître une forme plutôt qu’une donnée précise, nous avons besoin d’unifier deux expressions.

C’est le mécanisme que prolog utilise pour tenter de faire correspondre un fait et une règle pour savoir si la règle s’applique et pour créer un environnement local avec les noms de variables des prémisses de la clause.

C’est aussi le mécanisme que l’on utilise pour réaliser l’inférence de type dans les langages comme ML.

L’unification de deux expressions peut soit échouer car les deux structures sont incompatibles, soit réussir et produire un nouvel environnement local avec des nouvelles variables permettant de relier les données des deux expressions.

5.2.2 Reconnaissance d’un motif dans un texte

Le problème que nous évoquons ici est celui que traitent les éditeurs de textes pour nous permettre de retrouver un mot particulier. Nous pourrons étendre le problème à la reconnaissance d’expressions régulières ou à la reconnaissance de sous arbres dans un arbre.

Dans la suite nous parlerons donc de reconnaître un motif dans un texte et nous noterons n la longueur du texte et p la longueur du motif.

Nous supposerons toujours que p est négligeable devant n.

5.2.2.1 Soyons naïfs ! (en n x p)

Voici tout d’abord l’algorithme naïf (en anglais : brute force algorithm). Trouver le mot dans le texte, c’est d’abord être capable de dire si le texte commence par le motif (fonction le-mot-est-la dans l’exemple qui suit). Si le mot n’est pas là, nous irons le chercher plus loin. Simple, non ?

(de recherche-naive (motif texte)
    (cond ((null texte) ())
          ((le-mot-est-la motif texte) t)
          (t (recherche-naive motif
                             (cdr texte)))))
(de le-mot-est-la (motif texte)
    (cond ((null motif) t)
          ((null texte) ())
          ((eq (car motif) (car texte))
           (le-mot-est-la (cdr motif)
                          (cdr texte)))
          (t ())))

Exemple 5.2.2.1 recherche naïve (Lelisp)

int le_mot_est_la(char*motif,char*texte) {
  if(*motif==0)
    return 1;
  else if(*texte==0)
    return 0;
  else if(*motif==*texte)
    return le_mot_est_la(motif+1,texte+1);
  else
    return 0;
}
int recherche_naive(char*motif,char*texte) {
  if(*texte==0)
    return 0;
  else if(le_mot_est_la(motif,texte))
    return 1;
  else
    return recherche_naive(motif,texte+1);
}

Exemple 5.2.2.2 recherche naïve (C)

Ici, je profite honteusement de la structure des chaînes en C pour me promener dans les char* comme dans les listes chaînées : * pour avoir la tête et +1 pour la suite^⁵⁹.

Dans les deux exemples précédents, nous pourrions rendre une information plus riche qu’un simple booléen : pour pouvoir l’utiliser dans un éditeur de texte, il suffirait de rendre la référence à l’emplacement où on trouve le motif.

C’est un très bon algorithme, très facile, mais qui nécessite des retours en arrière.

De plus, le pire des cas (recherche de aaaab dans aaaaaaaaaaaaaab) nécessite n x p opérations, car il faut tester toutes les lettres du motif avant de trouver un échec, puis on est obliger de recommencer en se décalant d’une lettre seulement.

Evidemment, on se trouve rarement dans le pire des cas. La complexité moyenne pratique d’un tel algorithme dépend tout d’abord du contexte d’utilisation. Il nous faut cerner l’alphabet de travail. Plus l’alphabet est grand plus cet algorithme est bon. Sa simplicité de mise en œuvre est sa meilleure arme face aux deux algorithmes qui suivent.

5.2.2.2 Plus fort : L’automate KMP (en n)

Il arrive que l’on ne puisse en aucun cas faire de retour en arrière. C’était le cas lorsque l’information était stockée sur une bande magnétique comme pour le tri interclassement monotone. C’est aussi le cas pour un flux de données que l’on ne stocke pas (message émis par radio par exemple).

Il nous faut une technique qui ne nécessite qu’une seule lecture de chaque caractère. La technique qui fut proposée par messieurs Knuth, Morris et Pratt est aussi une très bonne technique pour des alphabets de cardinal réduit.

Les exemples qui suivent seront dans un alphabet binaire. Nos motifs et nos textes seront formés de « 0 » et de « 1 ».

Une analyse préliminaire du motif permet de garder toute l’information due à la lecture du texte. Nous allons définir une succession de p+1 états numérotés de 0 à p. Chaque état i correspond au fait que l’on a reconnu les i premières lettres de notre motif.

Pour le mettre en œuvre, il faut déjà comprendre le tableau suivant, construit pour le motif « 010010 » :

état - lettres lues	« 0 »	« 1 »
0 -	1 ok	0
1 - 0	1	2 ok
2 - 01	3 ok	0
3 - 010	4 ok	2
4 - 0100	0	5 ok
5 - 01001	6 ok	0
6 - 010010	4	2

Tout d’abord, les états marqués d’un ok correspondent à la lecture de la bonne lettre. On passe alors dans l’état suivant.

Lors de la lecture de l’autre caractère, c’est là que le prétraitement va nous permettre de gagner : au lieu de retomber à l’état 0, il est possible de reconnaître une portion du motif.

Lisons par exemple la ligne de l’état 3. Nous avons reconnu « 010 », nous espérons donc un « 0 » pour passer à l’état 4, mais nous recevons un « 1 ». On peut considérer que la chaîne lue (« 0101 ») correspond à deux caractères quelconques suivis du début du motif : « 01 ». On passe donc dans l’état 2, quitte à retomber plus bas si la suite est encore un « 1 ».

Nous avons gagné par rapport à l’algorithme naïf : d’une part, notre algorithme est exactement linéaire en n (une opération par lettre) et d’autre part, il ne nécessite aucun retour en arrière et il est donc acceptable pour la reconnaissance en temps réel.

5.2.2.2.1 Utiliser l’automate

C’est la partie la plus simple, du moins si on connaît d’avance l’alphabet de travail. Nous utiliserons les structures de contrôle dont nous parlions dans la section précédente. Ensuite, tout dépend de la structure que nous avons choisie pour représenter la table de l’automate.

En Pascal, je propose un tableau à deux dimensions ayant en indice d’une part, les p+1 états et d’autre part les lettres de notre alphabet.

type
  etat=[0..p];
  Automate=array[0..p,’0’..’1’];
procedure kmp(A:Automate;T:Texte);
var
  e:etat;
begin
  e:=0;
  while not fin(T) do
    begin
      e:=A[e,lire(T)];
      if e=p then
        motif_reconnu();
    end
end;

Exemple 5.2.2.3 utiliser l’automate (Pascal)

Dans cet exemple, le texte est manipulé par les fonctions fin qui rend vrai lors de la fin du texte et lire qui rend la lettre courante du texte et passe à la suivante.

En Lelisp, le selectq n’évaluant pas son deuxième argument qui est une liste de clause que nous construisons ici dynamiquement, nous sommes obligés d’utiliser apply pour forcer l’évaluation dynamique. On pourrait aussi utiliser la structure des plist avec les fonctions putprop et getprop.

(de kmp (automate texte)
  (let ((etat 0))
    (while texte
      (setq etat
        (apply ’selectq
          (cons (car texte)
                (apply ’selectq
                       (cons etat automate)))))
      (setq texte (cdr texte))
      (when (= etat p)
            (reconnaissance)))))

Où l’automate vu précédemment (pour « 010010 ») aurait la forme suivante :

((0 (0 1) (1 0) (t 0))
(1 (0 1) (1 2) (t 0))
(2 (0 3) (1 0) (t 0))
(3 (0 4) (1 2) (t 0))
(4 (0 1) (1 5) (t 0))
(5 (0 6) (1 0) (t 0))
(6 (0 4) (1 2) (t 0)))

Les (t 0) ne sont là que pour traiter le cas de lettres qui ne sont pas dans l’alphabet binaire que nous avons supposé.

Exemple 5.2.2.4 interpréter l’automate (Lelisp)

Encore une fois, il n’est pas vraiment nécessaire de proposer d’équivalent en Java car la classe String est déjà munie de toutes les méthodes imaginables et fortement optimisées. Les reprogrammer est une garantie de faire moins efficace et probablement d’y rajouter des erreurs.

5.2.2.2.2 Construire l’automate

En fait, c’est beaucoup plus facile qu’il n’y parait. Si la lettre est la bonne, la case correspondante du tableau est l’état courant plus 1. Si ce n’est pas la bonne, on sait que le motif ne peut être plus à gauche que la position courante et on sait que la position courante n’est pas bonne non plus. Donc, on reprend la lecture des etat premières lettres du motif en sautant la première et en y ajoutant la mauvaise lettre. On réutilise les etat-1 premières lignes de l’automate qui viennent d’être calculées pour trouver l’état suivant.

(defvar automate ‘((0 (,(tete motif) 1) (t 0))))
(de construit (n)
    (if (> n (length motif))
        () ;c’est fini
        (nconc1 automate
                ‘(,n ,(ligne n motif alphabet)))
        (construit (+ n 1))))
(de ligne (etat motif alphabet)
    (if (null alphabet)
        ’((t 0))
        ‘((,(car alphabet)
           ,(if (eq (car alphabet) (car motif))
                (+ etat 1) ;c’est la bonne lettre
                (kmp automate
                     (append
                      (cdr (firstn etat motif))
                      (list (car alphabet))))))
          ,(ligne etat motif (cdr alphabet)))))

Exemple 5.2.2.5 construction de l’automate (Lelisp)

C’est assez abscons, même pour un fervent lispien. L’utilisation des « ‘ » permet d’éviter de nombreux appels explicite à cons et list. C’est plus concis, mais j’ai bien peur que cela ne soit pas du plus lisible.

L’important, c’est l’idée que chaque ligne est construite à partir des lignes précédentes.

8.2.2.3Terrifiant : Boyer - Moore (en n / p)

Lorsqu’il n’y a aucune limitation pour les retours en arrière, il est possible de faire des recherches encore plus efficaces. Messieurs Boyer et Moore ont pensé à commencer les recherches par la fin du motif afin, lorsqu’on tombe sur une lettre étrangère au motif de pouvoir sauter en avant de la longueur du motif.

Dans le cas de l’utilisation d’un alphabet nombreux (c’est le cas pour l’édition de texte), il est courant de tomber sur une lettre ou un symbole qui ne fait pas partie du motif. La complexité pratique est alors proche de n/p, ce qui est bien meilleur que les algorithmes précédents.

Cette méthode demande un prétraitement assez simple : il faut remplir le tableau des décalages. Pour chacune des lettres de l’alphabet du motif, il va falloir compter de combien il faut décaler le motif vers la droite pour qu’il tombe en face de la lettre lue.

Ensuite, on commencera la comparaison par la fin du motif. Si le texte ne correspond pas, on avancera dans le texte du décalage correspondant dans le tableau.

Expliquons au travers d’un exemple. Nous cherchons le mot « tempete » dans la phrase « Le capitaine est accule par la tempete. » J’ai ignoré les accents dans le mot recherché pour bien montrer tous les cas.

Le tableau des décalages est :

Lettre	t	e	m	p	*
Décalage	1	2	4	3	7

Sur un exemple où il n’y aurait pas eu de répétition de lettres dans le mot, c’eut été plus simple de voir la règle générale qui s’applique ici pour le m et le p. Pour le t, nous pourrions nous décaler de 6 pour faire correspondre le t que nous venions de lire au premier t du mot, ratant ainsi la possibilité que ce soit le deuxième t. Plus compliqué, le cas du e : il n’est plus possible que ce soit le dernier e du mot car la comparaison a échoué. C’est donc le prochain e en allant vers la gauche. Le décalage est donc de 2.

Pour toutes les autres lettres, on se décalera d’une longueur de motif (ce qui est représenté par la colonne *).

Déroulons l’algorithme sur notre exemple.

Le capitaine est accule par la tempete.
tempete +7
       tempete+7
              tempete+7
                     tempete+7
                            tempete+3
                               tempete !

Il faut 6 étapes seulement pour tomber en face du mot tempete et ensuite il suffira des 7 comparaisons pour vérifier qu’il est bien là.

5.2.3 Les arbres de décision

Pour reconnaître des structures plus complexes comme des sous arbres syntaxiques, il faut souvent faire un longue succession de tests pour savoir dans quel cas on se trouve.

Ce genre de programme peut s’optimiser en factorisant les tests ou en créant des automates avec des structures d’états plus complexes que celles vues pour nos automates KMP.

Ces problèmes donnant lieu à des programmes quelques peu compliqués, je ne m’étalerai pas ici dans la programmation. Mais il est important, lorsqu’un programme présente de nombreux cas avec des successions de test, de consacrer un peu de temps à l’optimisation des tests. Il faut séparer tous les cas, puis isoler les différences les plus caractéristiques pour commencer à tester les critères les plus significatifs.

Ce paragraphe est ici, car il s’agit de problèmes de reconnaissance d’arbre, mais il aurait pu figurer dans le chapitre des optimisations (il eût alors fallu que je le développe et cela aurait pris encore une dizaine de pages…).

5.3 Divers autres problèmes

Evidemment, nous avons suffisamment traité de problèmes pour l’instant, mais je ne résiste pas à l’envie de citer quelques autres problèmes récurrents dans les applications que j’ai eu à développer.

5.3.1 La simulation

Il est souvent nécessaire de simuler le comportement humain, afin de prendre des décisions (Combien faut-il ouvrir de caisses au supermarché le samedi après-midi pour maximiser le profit ?) (Quelle est la vitesse limite qui donne le meilleur débit sur le boulevard périphérique parisien ?). On simule parfois aussi des situations informatiques pour aider dans la conception d’un réseau ou pour évaluer un protocole de communication (Qu’arrive-t-il si 500 ordinateurs se connectent en même temps ?).

On a mis au point de nombreuses techniques pour la simulation (la programmation par acteur par exemple) mais lorsqu’on modélise le comportement humain comme lorsqu’on modélise une loi physique, il y a une seule chose à ne jamais perdre de vue.

Il ne s’agit pas d’expliquer la réalité, mais de modéliser. Si vous utilisez une formule qui vous semble correcte mais qui ne donne pas le bon résultat, préférez lui la fonction empirique et inexplicable mais qui simule bien.

5.3.2 Les jeux et l’aide à la décision

Je citerai sans développer, les réseaux de neurones, les algorithmes génétiques et certains systèmes experts qui permettent de créer des programmes d’aide à la décision qui apprennent de leurs erreurs.

On utilise ces algorithmes et techniques pour la programmation des jeux. On y verra aussi de nombreuses variantes du Min Max, comme αβ vu précédemment, mais aussi Scout qui est une sorte de mémofonction de Min Max.

6 Représenter l’information

Comme on l’a déjà dit au début, c’est un des problèmes cruciaux dans la conception d’un algorithme. Avec nos nombreuses structures de données, on peut représenter n’importe quoi. Mais comment peut-on trouver la représentation adaptée au problème ?

Le choix de ce qui va être représenté, le choix du type abstrait, puis du langage et de la représentation physique, des éventuelles tolérances d’erreur... tous ces choix sont autant de raisons d’avoir une méthode.

De toute façon, il n’y a pas de recette miracle, mais voici une petite méthode sur laquelle se rabattre, lorsqu’on manque d’idées.

D’abord, représenter toutes les informations avec des dessins. On doit ainsi s’affranchir du langage et de ses particularités et éviter de s’imposer un choix trop tôt.
Isoler l’information de départ et d’arrivée.
Concevoir un algorithme en langage naturel et dessiner le chemin de l’information (diagramme de flot de données).
En déduire l’information utile, évitant ainsi le gaspillage de temps et de place.
Vérifier l’absence de redondance dans l’information entrante, principale source d’incohérence (on pourra sauvegarder les informations calculées plus tard pour gagner du temps). Une information est considérée redondante, si on peut la recalculer à partir d’autres informations entrantes.
Et alors seulement, choisir une implantation.

6.1 Modéliser n’importe quoi

Tout objet ou idée fini peut être représenté. Si on peut l’imaginer, si on peut le dessiner, alors on peut le représenter dans notre machine.

Dans la section qui suit, nous découvrons un exemple tiré d’un problème purement spéculatif au départ. Notre idée était de représenter un sous-ensemble des chaînes de caractères, pour pouvoir décrire un ensemble de personnes de manière générale. Il s’agissait d’exprimer des critères de recherche dans un annuaire en permettant d’élargir ou de restreindre la recherche (union et intersection d’ensembles vérifiant des critères sur l’ordre lexicographique)

6.1.1 Union d’intervalles

Notre contexte de départ était un fichier contenant des informations sur des personnes, notamment leurs noms, prénoms et numéros de téléphone. Supposant que le fichier pouvait contenir un nombre important de personnes et que ces personnes pouvaient être représentées par un nombre important d’informations, il paraissait difficile d’en décrire une exhaustivement pour une quelconque manipulation.

Nous voulions donc créer un langage de communication avec le fichier pour pouvoir accéder aux informations qu’il contenait de manière « intelligente » QQCVD.

En fait nous avons commencé par poser le problème en termes de recherche. Notre utilisateur voulait pouvoir décrire un ensemble de noms, un ensemble de prénoms et autres pour décrire un ensemble de personnes.

Il voulait pouvoir éditer ces ensembles pour étendre ou affiner sa recherche. Nous avons donc restreint notre problème à la représentation d’un seul ensemble de chaînes de caractères, sachant qu’il serait facile de l’étendre au problème complet. Le type abstrait suivant est construit pour décrire ses besoins.

Sorte : Ensemble

Utilise : (Chaîne, <), Saisie_Utilisateur

Opérations :

affiner : Ensemble, Saisie® Ensemble
étendre : Ensemble, Saisie® Ensemble
 : ® Ensemble
Tout : ® Ensemble

Type abstrait 6.1.1.1 ensemble vu par l’utilisateur

On pourrait très bien construire ce type abstrait sur un type un peu plus formel qui est plus proche de nos souvenirs de maths modernes.

Sorte : Ensemble

Utilise : (Chaîne, <)

Opérations :

 : Ensemble, Ensemble ® Ensemble
 : Ensemble, Ensemble ® Ensemble
 : ® Ensemble
Tout : ® Ensemble
Saisie : ® Ensemble (Pour une fois il ne s’agit pas d’une constante mais d’un accès à l’environnement externe)

Axiomes : Les axiomes du type abstrait sont les propriétés caractéristiques de l’objet et en l’occurrence, ces propriétés sont trop nombreuses ici pour être d’un quelconque intérêt pour la programmation.

Type abstrait 6.1.1.2 ensemble formalisé de manière plus classique

On peut aussi rajouter une opération : suppression : Ensemble, Ensemble ® Ensemble

On pourra considérablement simplifier le travail grâce à la fonction : complémentaire : Ensemble ® Ensemble

Sachant que

A  B = C(C(A)  C(B))
A – B = A  C(B) = C(C(A)  B)
Tout = C()

Il nous reste maintenant à décrire l’ensemble élémentaire. La première idée qui nous est venue est l’intervalle.

En effet, il peut être intéressant de sélectionner les mots compris entre deux valeurs. Pour respecter la stabilité de notre opération, il nous faut décrire une union d’intervalles. Car si on étend l’intervalle [mot1,mot2] à l’aide de l’intervalle [mot3,mot4] et que nos valeurs sont telles que les deux intervalles sont disjoints, le résultat doit être représentable sous forme d’ensemble.

Immédiatement, le cerveau bien huilé du programmeur se met en marche. Il visualise la demi-droite qu’est l’ensemble des chaînes de caractères et y pose des segments limités par des crochets ouverts et fermés.

Malheureusement, il oublie vite cette conception visuelle. La première chose qu’il imagine alors, c’est une liste d’intervalles. Les intervalles sont alors des enregistrements de quatre informations : les valeurs des deux bornes (deux chaînes), et le fait qu’elles soient ouvertes ou fermées (deux booléens).

Dès les premières tentatives d’implantation, le programmeur constate que quelque chose ne va pas : les fonctions deviennent très vite trop compliquées et elles sont pleines de cas particuliers. Pourtant, le problème semblait simple.

C’est donc la conception qui est en cause ! En fait, une solution beaucoup plus simple découle de cette visualisation de départ.

Il nous faut représenter une liste de bornes plutôt qu’une liste d’intervalle. Si ce sont des Listes_triées (cf. Type abstrait 5.1.1.1) alors, l’union ne serait qu’une fusion (cf. Exemple 5.1.1.11) éventuellement suivie d’une simplification des bornes en trop.

Il ne nous manque donc plus qu’un type borne.

Sorte : Borne

Utilise : Chaîne, Booléen

Opération :

< : Borne, Borne ® Booléen
Cons_Borne : Chaîne, Booléen, Booléen ® Borne
Valeur : Borne ® Chaîne
Borne_inf? : Borne ® Booléen
Ouverte? : Borne ® Booléen

Type abstrait 6.1.1.3 borne

Nous ne sommes pas encore à même de décrire une relation d’ordre rigoureuse sur notre ensembles de bornes. Mais par contre, en le projetant sur l’espace des valeurs, on peut tout simplement utiliser l’ordre lexicographique.

Ce n’est pas une relation d’ordre, car il nous manque l’antisymétrie dans le cas de deux bornes définies sur la même valeur mais ayant des caractéristiques différentes.

Avec cette relation d’ordre, nous pourrons implanter le type abstrait liste_de_bornes sur lequel nous construirons notre type ensemble.

Sorte : Liste_de_borne

Utilise : Borne

Opérations :

Type abstrait 6.1.1.4 liste de bornes

Si l’on considère que Saisie nous rend une liste de deux bornes représentant une intervalle, on peut facilement démontrer que la fusion conserve la propriété suivante :

Les listes sont des expressions bien parenthèsées. Ce qui signifie les deux propriétés suivantes :

Il y a autant de bornes supérieures que de bornes inférieures.
Si on lit la liste de gauche à droite, on a toujours lu au moins autant de bornes inférieures que de bornes supérieures.

Il est indispensable pour que nos listes aient un sens que nous alternions borne inférieure et borne supérieure. Cette propriété de « bon parenthésage » de nos listes est très intéressante, mais elle n’est pas suffisante pour garantir l’unicité de la représentation d’un ensemble. La représentation canonique serait une liste de ce type dans laquelle il n’y aurait aucune imbrication.

Grâce à ce type liste_de_bornes, il nous est alors possible de programmer notre simplification des bornes en trop (celles qui sont imbriquées) comme dans l’exemple suivant.

Ainsi nous aurons effectivement le type ensemble avec la propriété importante suivante :

Un ensemble est une suite alternée de bornes inférieures et supérieures commençant par une borne inférieure et finissant par une borne supérieure.

function simplification(l:liste):liste;
  function simplif_aux(l:liste;
                       niveau:integer)
                         :liste;
  begin
    if vide(l) then
      return(l)
    else
      if Borne_inf(tete(l)) then
        if niveau=0 then
          return(cons(tete(l),
                      simplif_aux(suite(l),
                                  niveau+1)))
        else
          return(simplif_aux(suite(l),
                             niveau+1))
      else
        if niveau=1 then
          return(cons(tete(l),
                      simplif_aux(suite(l),
                                  niveau-1)))
        else
          return(simplif_aux(suite(l),
                             niveau-1))
  end;
begin
  return(simplif_aux(l,0)
end;

Exemple 6.1.1 9.1.1.1 simplification des imbrications (Pascal)

La variable niveau sert à comptabiliser le niveau d’imbrication. On ne garde que les bornes utiles, celles qui font passer de 0 à 1 ou de 1 à 0.

Nous avons, grâce à cette fonction de simplification, implanté l’union d’intervalles : il suffit de saisir des intervalles, de les fusionner et de les simplifier comme dans l’exemple suivant :

function union(A,B:liste):liste;
begin
return(simplification(fusion(A,B)))
end;

Exemple 6.1.1.2 union d’intervalles (Pascal)

C’est alors que l’on découvre le véritable problème lié aux bornes.

Nous ne savons pas, avec notre actuelle relation d’ordre, faire l’union de deux ensembles adjacents. Le problème est entièrement contenu dans la non antisymétrie de notre fonction inférieur appelée dans la fusion.

Il va nous falloir définir la table de vérité de la relation < entre les bornes définies sur la même valeur a. On peut prendre certaines décisions en ce disant qu’une borne est une coupure qui a lieu à gauche ou à droite de notre valeur (une borne inférieure fermée est à droite, ainsi qu’une ouverte supérieure, les autres sont à gauche).

B1 \ B2	]---	[---	---[	---]
]---	V	F	F	?
[---	V	V	?	V
---[	V	?	V	V
---]	?	F	F	V

Figure 6.1.1.1 table de la relation d’ordre

Il y a encore un problème sur la diagonale opposée : on ne voit pas d’ordre à priori. Mais pour que ces bornes disparaissent à la simplification, il est nécessaire de les faire se recouvrir (c’est alors la borne inf qui est la plus petite). On peut alors programmer notre relation d’ordre comme dans l’exemple suivant :

function inferieur(b1,b2:borne):boolean;
begin
  if valeur(b1)<>valeur(b2) then
    return(valeur(b1) < valeur(b2))
  else
    if meme_borne(b1,b2) then
      return(true)
       {reflexive}
    else
      if meme_borne(b1,
                    inverse_borne(b2)) then
        return(borne_inf(b1))
          {recouvrement}
      else
        return(borne_inf(b1) = ferme(b1))
end;

Exemple 6.1.1.3 relation d’ordre correcte (Pascal)

6.2 Adapter sa représentation

Les représentations naïves sont souvent les meilleures, mais parfois, il arrive que l’on ne soit pas satisfait. Par exemple, ayant écrit une superbe mémofonction pour le factoriel (cf. Exemple 4.1.2.1), l’utilisateur voudrait calculer le nombre de combinaisons de 800 éléments dans 400 places.

Premier échec, c’est trop grand pour les entiers de la machine. Deuxième échec, c’est même trop grand pour les flottants de sa machine !

Pourtant, c’est un auxiliaire de calcul indispensable pour notre utilisateur (c’est un fou des nombres, et il voudrait savoir comment ceux-ci se comportent).

6.2.1 Combinaisons

La curiosité, ou tout autre prétexte plus légitime, nous pousse donc à chercher une représentation des nombres qui nous permette de travailler correctement.

Mais ici, notre problème n’est pas quelconque : en effet, nos nombres ont surtout besoin d’être multipliés entre eux. On pourrait par exemple les représenter par la liste de leurs chiffres. Je vous laisse alors imaginer la fonction de multiplication (facile à écrire peut-être, mais diablement inefficace).

Non ! Il nous faut une représentation adaptée aux multiplications. Pourquoi ne pas les représenter par leur décomposition en facteurs premiers ? La multiplication deviendrait alors une série de somme d’indices, la division une série de différences.

Pour être plus concret : 200=2³x3⁰x5² serait représenté par la liste (3 0 2), 12=2²x3¹ par (2 1) et donc leur produit 2400 serait représenté par la liste (5 1 2).

Utilisons donc notre liste des nombres premiers définie dans l’Exemple 4.1.4.1, avec la fonction suivant. Définissons la décomposition en facteurs premiers.

(de decomposition (n)
  (decomp-aux n premier-des-premiers))

(de decomp-aux (n facteur)
  (cond ((= 1 n) ())
        (t
         (cons (exposant facteur n)
               (decomp-aux
                  (divis n facteur)
                  (suivant facteur))))))

(de exposant (facteur n)
  (cond ((<> 0 (modulo n facteur)) 0)
        (t (+ 1
              (exposant facteur
                        (div n facteur))))))

(de divis (n facteur)
  (cond ((<> 0 (modulo n facteur)) n)
        (t (divis (div n facteur)
                  facteur))))

exposant nous donne l’exposant d’un facteur dans un nombre, divis rend le nombre privé de ce facteur (divisé par le facteur élevé à exposant).

Exemple 6.2.1.1 décomposition en facteurs premiers (Lelisp)

Avec cet exemple, il ne nous est plus très difficile de passer à notre calcul des combinaisons avec un « mémo-factoriel ».

(de combinaison (n p)
  (division (factoriel n)
            (multiplication
              (factoriel (- n p))
              (factoriel p)))))

(de multiplication (l1 l2)
  (cond ((null l1) l2)
        ((null l2) l1)
        (t (cons (+ (tete l1) (tete l2))
                 (multiplication
                   (suite l1)
                   (suite l2))))))

(de division  (l1 l2)
  (cond ((null l2) l1)
        (t (cons (- (tete l1) (tete l2))
                 (division (suite l1)
                           (suite l2))))))

(plist ’factoriel ’(0 ()))
(de factoriel (n)
  (cond ((getprop ’factoriel
                  n))
        ((putprop ’factoriel
                  (multiplication
                    (factoriel (- n 1))
                    (decomposition n))
                  n))))

Exemple 6.2.1.2 combinaisons (Lelisp)

Notez au passage que nous ne définissons pas la valeur de la division dans le cas où on épuiserait la liste du dividende avant celles du diviseur.

En fait, cela correspondrait à une division non entière, ce qui ne peut pas arriver dans notre exemple, car le nombre de combinaisons est forcément un entier naturel.

6.2.2 Polynômes

Comme pour représenter les nombres avec leur décomposition première, le problème des polynômes demande en premier lieu une forme canonique, qui garantisse l’unicité de la représentation.

Deux alternatives apparaissent immédiatement :

Si le corps est algébriquement clos, alors on peut les représenter par leur décomposition en polynômes premiers (de degré 1). Moyennant un hachage adapté, les calculs de la multiplication, du pgcd et autres deviennent très rapides. C’est le choix fait par MAPLE, le célèbre logiciel de calcul formel.
Sinon il nous reste toujours la forme développée, beaucoup plus simple à calculer.

Nous ferons ici le deuxième choix dans le cadre de la représentation de polynômes à coefficients réels.

Nous allons naturellement utiliser les listes. Mais une fois de plus nous avons un choix déterminant à faire entre les deux possibilités suivantes.

Une liste de monômes. Chaque monôme étant représenté par un couple d’informations (coefficient,degré). L’ordre n’est pas alors important. 1+3X² serait alors représenté par la liste : {(1,0);(3,2)}
Une liste de coefficients. Le degré de chaque monôme correspondant alors à la position du coefficient dans la liste : 1+3X² serait alors représenté par la liste : {1;0;3}

Si les coefficients ne sont que rarement nuls, la première solution est la plus économique en place mémoire. Mais si celle-ci est parfois plus facile à programmer, les erreurs sont plus difficiles à diagnostiquer car toute l’information n’est pas présente (Le degré d’un monôme dépend de sa position dans la liste et elle est donc liée au parcours).

Le deuxième choix est donc motivé par des considérations de développement plus convivial, et non pour des raisons d’efficacité.

Le type abstrait polynôme utilise le type monôme. Le type abstrait liste peut être utilisé tel quel pour les polynômes :

Sorte : Monôme

Utilise : Réel, Entier

Opérations :

Cons_monôme : Réel, Entier ® Monôme
Degré : Monôme ® Entier
Coefficient : Monôme ® Réel

Type abstrait 6.2.2.1 monôme

Sorte : Polynôme

Utilise : Monôme, Booléen

Opérations :

Cons : Monôme, Polynôme ® Polynôme
Suite : Polynôme ® Polynôme
Tête : Polynôme ® Polynôme
Vide? : Polynôme ® Booléen
Zéro : ® Polynôme

Type abstrait 6.2.2.2 polynôme

6.2.2.1 Addition

Comme on peut le voir dans l’exemple qui suit, il n’est pas trop difficile de définir l’addition, si on suppose que les listes de monômes sont triées par ordre croissant des degrés. C’est à peu de choses près la fusion des listes triées (cf. Exemple 5.1.1.11).

function addition(p1,p2:polynome);
begin
  if vide(p1) then
    return(p2)
  else if vide(p2) then
    return(p1)
  else if degre(p1)<degre(p2) then
    return(cons(tete(p1),
                addition(suite(p1),
                         p2)))
  else if degre(p1)>degre(p2) then
    return(cons(tete(p2),
                addition(p1,
                         suite(p2))))
  else {alors degre(p1)=degre(p2)}
    return(cons(cons_monome(coefficient(p1) +
                            coefficient(p2),
                            degre(p1)),
                addition(suite(p1),
                         suite(p2))))
end;

Exemple 6.2.2.1 addition de polynômes (Pascal)

Dans le cas où nous aurions choisis la représentation en liste de coefficient, le travail eût été plus simple : nous n’aurions pas eu à comparer les degrés. C’est exactement la fonction de multiplication des nombres décomposés dans l’Exemple 6.2.1.2.

6.2.2.2 Multiplication

N’ayant pas d’idée extraordinaire pour simplifier le calcul, je propose de faire le calcul de la manière simple, en deux temps.

D’abord la multiplication d’un polynôme par un monôme :

function multiplie_monome(m:monome;
                          p:polynome):polynome;
begin
  if vide(p) then
    return(liste_vide)
  else
    return(cons(cons_monome(coefficient(m)*
                            coefficient(tete(p)),
                            degre(m)+
                            degre(tete(p))),
                multiplie_monome(m,
                                 suite(p))))
end;

Puis on définit le produit :

function multiplication(p1,p2:polynome)
             :polynome;
begin
  if vide(p1) then
    return(liste_vide)
  else
    return(addition(
             multiplie_monome(tete(p1),p2),
             multiplication(suite(p1),p2)))
end;

Exemple 6.2.2.2 multiplication de polynômes (Pascal)

6.2.3 Retour sur les arbres binaires de recherche

6.2.3.1 Rééquilibrage automatique

Le problème de nos arbres vient, comme pour l’exemple du tri rapide (cf. Exemple 5.1.1.14), du fait que les objets arrivent parfois de manière partiellement triée. Dans les arbres binaires, cela donne lieu à des arbres déséquilibrés. Au lieu d’avoir une recherche équivalente à une dichotomie, on se retrouve avec une recherche linéaire.

Il nous faudrait rééquilibrer les arbres pour que leur profondeur reste de l’ordre de log(n) au lieu de n.

Pour réaliser des transformations dans l’arbre tout en gardant les propriétés de l’ordre des éléments, nous allons définir d’abord la rotation gauche et la rotation droite.

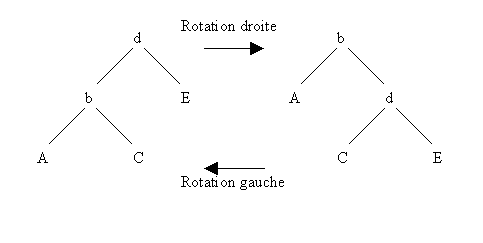
rotations simples

Figure 6.2.3.1 rotations simples

Si nous avons un arbre qui est déséquilibré à gauche, nous ferons une rotation droite et vice versa. Mais ça ne suffit pas : le sous arbre C dans la figure est resté à la même profondeur. Il nous faut donc prévoir deux opérations plus complexes qui sont les rotations gauche-droite et droite-gauche.

rotation droite-gauche

Figure 6.2.3.2 rotation droite-gauche

Il faut maintenant programmer ces rotations à l’aide de nos dessins. Il y a évidemment deux choix : d’une part, on peut construire effectivement le nouvel arbre, ou bien on peut reconstruire le chaînage.

La première méthode, non destructive, pourrait donner pour la rotation gauche :

function rotation_gauche(a:arbre):arbre;
begin
  return(cons(tete(droit(a)),
              cons(tete(a),
                   gauche(a),
                   gauche(droit(a))),
              droit(droit(a))))
end;

Exemple 6.2.3.1 rotation gauche logique (Pascal)

La deuxième méthode, plus économique en mémoire, mais destructive de son argument, peut être programmé ainsi dans la classe Arbre de Java :

void rotationGauche() {
  Element b=this.tete;
  Arbre A=this.gauche;
  this.tete=this.droit.tete;
  this.gauche=this.droit;
  this.gauche.tete=b;
  this.droit=this.gauche.droit;
  this.gauche.droit=this.gauche.gauche;
  this.gauche.gauche=A;
}

Exemple 6.2.3.2 rotation gauche physique (Java)

Malheureusement, pour effectuer les rééquilibrages, il faudrait faire les rotations au fur et à mesure des insertions, lorsqu’on découvre un déséquilibre. Cela nécessite de parcourir l’arbre à la recherche de la profondeur. C’est facile à programmer, mais cela rend l’insertion très coûteuse :

int profondeur(t_arbre a) {
  if(vide(a))
    return -1;
  else
    return 1+max(profondeur(gauche(a)),
                 profondeur(droit(a)));
}

Exemple 6.2.3.3 profondeur d’un arbre (C)

La valeur -1 pour la profondeur de l’arbre vide est conventionnelle. J’aurais évidemment préféré la valeur 0, mais plions nous aux conventions, cela évite les confusions.

Il nous faut donc faire n appels récursifs pour un arbre à n éléments. Comme ce calcul est nécessaire pour calculer le déséquilibre en un nœud (c’est la profondeur du fils droit moins la profondeur du fils gauche), nous allons calculer et recalculer ces valeurs de nombreuses fois. Il nous faut donc une mémofonction.

Où allons nous stocker les informations sur la profondeur d’un nœud ? Sur le nœud lui-même, évidemment :

class Arbre {
  public Element tete;
  public Arbre gauche, droit;
  public int profondeur;

  public Arbre(Element tete,
               Arbre gauche,
               Arbre droit) {
    this.tete=tete;
    this.gauche=gauche;
    this.droit=droit;
    profondeur=1+max(profondeur(gauche),
                     profondeur(droit));
  }

  public int desequilibre() {
    return profondeur(droit)-profondeur(gauche);
  }

  public static int profondeur(Arbre a) {
    if(a==null)
      return -1;
    else
      return a.profondeur;
  }
}

Exemple 6.2.3.4 classe Arbre améliorée (Java)

Nous pouvons ainsi détecter les déséquilibres et agir dès l’insertion. Il est même possible de concevoir un constructeur qui rééquilibre automatiquement.

Le rééquilibrage ne peut pas produire des arbres parfaits (i.e. tous les nœuds ont un déséquilibre nul). En effet, un arbre parfait à nécessairement un nombre de nœuds égal à 2^p-1 où p est sa profondeur.

Par contre, nous pouvons garantir un déséquilibre en tout nœud compris entre -1 et 1. Voici une proposition de procédure de rééquilibrage d’un nœud :

public void reequilibrage() {
  if(this.desequilibre()<-1)
    if(gauche.desequilibre()>0)
      rotationGaucheDroite();
    else
      rotationDroite();
  else if(this.desequilibre()>1)
    if(droit.desequilibre()<0)
      rotationDroiteGauche();
    else
      rotationGauche();
  else
    //le noeud est déjà équilibré
}

Exemple 6.2.3.5 rééquilibrage d’un noeud (Java)

6.3 Ne représenter que ce qui est utile, sans redondance

Il ne s’agit pas seulement d’éviter les redondances mais aussi d’éviter les incohérences.

6.3.1 Le complémentaire de nos unions d’intervalles

Reprenons notre exemple de manipulation des intervalles. Il nous manque encore la possibilité de programmer l’intersection.

Après une première réflexion, il est clair qu’il ne nous est pas possible de programmer directement l’intersection en utilisant une autre fonction de simplification, car le choix que nous avons fait dans notre relation d’ordre sur la diagonale opposée est dédié à l’union.

Il faut donc que nous calculions l’intersection par le complémentaire de l’union des complémentaires.

Il suffirait alors de construire la liste des bornes inverses. Mais alors nous n’avons plus la propriété intrinsèque des ensembles (nous commençons par une borne supérieure et nous finissons par une borne inférieure). Nous utilisons partiellement cette propriété dans la simplification.

Il faut donc que nous représentions les extrêmes de notre complémentaire. L’ensemble des chaînes de caractères étant une demi-droite (["",+[), nous n’avons pas de problème pour représenter la borne zéro :

zero=cons_borne(’’,inferieur,ouverte);

Par contre la borne +[ ne peut être représentée (ce serait une chaîne formée d’une infinité de caractères 255).

Mais est-elle véritablement utile ? Oui et non. Il n’est pas nécessaire de la représenter car l’information de son existence peut être déduite par le fait que la liste se termine par une borne inférieure. D’autre part elle n’intervient pas dans la simplification.

On peut continuer à utiliser la liste représentant un ensemble en omettant de représenter la borne +[ mais en la gardant de manière fictive (Voyez l’affichage des ensembles cf. Exemple 6.4.1.3). Il suffit de trouver la parité du nombre de bornes (avec un booléen dedans par exemple dont la valeur alterne au fur et à mesure du parcours) et si elle est impaire, c’est qu’il manque la borne infinie.

Notre complémentaire devient alors une fonction qui rajoute la borne zéro si elle n’existe pas et qui l’enlève sinon et qui inverse l’ensemble des bornes qui composent le reste de la liste :

function complementaire(l:liste):liste;
  function inverse(l:liste):liste;
  begin
    if vide(l) then
      return(l)
    else
      return(cons(inverse_borne(tete(l)),
                  inverse(suite(l))))
  end;
begin
  if vide(l) or
     not meme_borne(zero,tete(l)) then
    return(cons(zero,inverse(l)))
  else   {c’etait deja un complementaire}
    return(inverse(suite(l)))
end;

Exemple 6.3.1.1 l’ensemble complémentaire (Pascal)

6.3.2 La représentation des nombres et des polynômes

Nous avons représenté des nombres entiers sous forme de produit de leur décomposition première et des polynômes sous la forme de la somme de monômes (cf. Exemple 6.2.1.1 et Exemple 6.2.2.1).

Dans les deux cas, nous avions le choix entre représenter des listes de paires (facteurs et exposants pour les entiers, coefficient et puissance pour les polynômes) et des listes simples (exposants pour les nombres et coefficients pour les polynômes).

Dans les deux cas, les listes de paires présentent une redondance dans le cas où les puissances ou les coefficients nuls sont nombreux. Comme les nombres premiers et les monômes pouvaient être rangés par ordre croissant, leur position dans la liste est suffisante pour les déterminer.

Le choix est donc dépendant de la fréquence des zéros dans la représentation :

Si on doit représenter des nombres comme 32767 qui vaut 7x31x151, la première technique donne une liste de trois paires alors que la deuxième donne une liste d’une trentaine de cellules dont seules trois ne valent pas 0.

La première technique est alors la plus intéressante, mais dans le cas de la représentation de factoriels, le moindre facteur premier est présent au moins une fois, ne serais-ce que pour lui-même. La deuxième technique consomme alors 2 fois moins de cellules. De plus, sa programmation est plus simple.

Le même type de résonnement doit être appliqué à nos polynômes. Pourtant, il y a une motivation supplémentaire qui peut faire pencher la balance vers le choix de la liste de paires :

La visualisation des données est plus facile si toute l’information et directement accessible.

6.4 Visualiser les données

Il y a de multiples raisons particulières à chaque programme de visualiser l’information à l’écran (informer l’utilisateur sur l’état des données, prévenir des erreurs ou tout simplement lui montrer que le programme tourne,). Mais du côté du développeur, il se trouve qu’il est crucial pour programmer de manière efficace d’avoir les moyens de visualiser les données. Visualiser les données d’entrée et de sortie de chaque entité à développer ou tester.

C’est indispensable lors du développement. C’est le premier outil de déboguage.

Je vais par la suite proposer systématiquement des fonctions d’affichage d’objets avec le profil :

affiche : Objet ® Objet

De plus, l’objet rendu sera l’objet passé en argument. Il s’agit de pouvoir insérer l’appel de la fonction dans n’importe quel calcul, sans changer la valeur de retour de celui-ci :

result=a+f(b+c,affiche(d+f(g,e)));

Nous avons le même effet que l’évaluation de :

result=a+f(b+c,d+f(g,e));

Avec l’affichage de la valeur d+f(g,e). Nous pouvons ainsi observer des intermédiaires de calcul de manière non intrusive, sans être obligé de déclarer une variable supplémentaire et de scinder l’instruction en deux parties.

Dans le langage Java, il y a toujours une solution simple car tous les objets dérivent de la classe universelle Object qui est munie de la méthode toString() qui produit leur représentation imprimable.

Si le développeur Java a le bon goût de surcharger cette fonction pour toutes ses classes, alors il dispose de l’intermédiaire de calcul idéal, et l’affichage universel devient :

public static Object affiche(Object o) {
System.out.println(o.toString());
return o;
}

Exemple 6.3.2.1 afficheur universel (Java)

Mais c’est d’un emploi pénible car le résultat étant de la classe Object, il faudra faire des conversions explicites. Mieux vaut rajouter des méthodes spécifiques à chaque classe.

6.4.1 Listes

Il y a évidemment deux possibilités : on peut les afficher dans l’ordre de parcours ou dans l’ordre de construction.

L’affichage des listes en Lelisp se fait avec un appel à (print l) qui a le bon goût de rendre l. Pour les avoir dans l’ordre inverse, on peut écrire (reverse (print (reverse l))) (le reverse externe est là pour remettre la valeur d’origine).

Par contre en C, nous écrirons :

t_liste affiche_liste(t_liste l) {
  if(vide(l)) {
  } else {
    affiche_element(tete(l));
    affiche_liste(suite(l));
  }
  return l;
}

Exemple 6.4.1.1 affichage des listes dans l’ordre de parcours (C)

Et pour l’ordre inverse :

t_liste affiche_liste(t_liste l) {
  if(vide(l)) {
  } else {
    affiche_liste(suite(l));
    affiche_element(tete(l));
  }
  return l;
}

Exemple 6.4.1.2 affichage des listes dans l’ordre de construction (C)

La valeur de retour ne sert qu’au niveau le plus élevé : dans les appels récursifs, la valeur n’est pas utilisée. Par contre, cela ne coûte rien en terme de temps d’évaluation.

L’affichage des éléments doit évidemment être réalisé aussi. Pour notre problème d’union d’intervalles (cf. Type abstrait 3.1.1.4 et l’Exemple 3.1.1.2), voici l’affichage des bornes et des ensembles :

procedure affiche_borne(b:borne);
begin
  if b.inf then
    if b.ouv then
      write(’ ’,b.val,’[’)
    else
      write(’ ’,b.val,’]’)
  else
    if b.ouv then
      write(’]’,b.val,’ ’)
    else
      write(’[’,b.val,’ ’)
end;

function affiche_ensemble(l:liste}:liste;
  procedure aff(l:liste;dedans:boolean);
  begin
    if vide(l) then
      if dedans then
        writeln(’ +oo[’)
      else
        writeln
    else
      begin
        affiche_borne(tete(l));
        aff(suite(l),not dedans)
      end
  end;
begin
  aff(l,false);
  affiche_ensemble:=l
end;

Exemple 6.4.1.3 affichage des ensembles (Pascal)

6.4.2 Arbres binaires

Pour les besoins du déboguage, il ne nous est pas nécessaire de faire appel à des procédures graphiques dépendantes de la machine. Il nous est encore possible d’utiliser les fonctions de base d’affichage de caractères.

Je vous propose ici une fonction d’affichage d’arbre non ambiguë et tout à fait satisfaisante si les objets à afficher ne sont pas trop larges.

function affiche_arbre(a:arbre):arbre;
  procedure aff_niveau(i:integer;a:arbre);
  begin
    if not vide(a) then
      begin
        aff_niveau(i-1,gauche(a));
        if i=0 then
          affiche(tete(a))
        else
          espace(tete(a));
        aff_niveau(i-1,gauche(a))
      end
  end;
var
  i:integer;
begin
  for i:=1 to hauteur(a) do
    begin
      aff_niveau(i,a);
      writeln
    end;
  affiche_arbre:=a
end;

Exemple 6.4.2.1 affichage d’arbre binaire (Pascal)

Où espace est une procédure qui affiche un espace de la largeur de la tête de l’arbre et affiche permet d’afficher un élément.

L’intérêt de cette procédure est qu’elle fonctionne sur toutes les consoles possibles dans tous les langages. On obtient un élément par colonne, placé à la bonne hauteur :

      4
  2         7
1   3     6   8
        5

C’est beaucoup plus lisible que l’ensemble des trois parcours, pour le même arbre :

parcours préfixe : 4 2 1 3 7 6 5 8
parcours infixe : 1 2 3 4 5 6 7 8
parcours postfixe : 1 3 2 5 6 8 7 4

6.4.3 Arbres quelconques, graphes

Il existe de nombreuses structures plus complexes à représenter mais qui sont très courantes. En premier lieu, les arbres n-aires. Leurs nœuds contiennent un ensemble d’information et un ensemble de fils.

Dans le domaine de la compilation, on représente ainsi les programmes et les nœuds peuvent représenter toutes les entités syntaxiques.

Par exemple, un nœud instruction « if then else » est un nœud à trois fils : l’expression qui lui sert de test, l’instruction pour le cas où le test est vrai et l’instruction pour le cas où le test est faux.

Le nœud peut aussi porter des informations sur l’environnement (quelles variables sont accessibles, quel est leur type, quel est le prochain registre que je peux affecter, etc.) et ces informations doivent pouvoir être visualisée.

On peut, pour les arbres véritablement complexes, imaginer un outil de visualisation nous permettant de nous promener dans la structure, mais cela nécessite une intervention humaine. Il nous faut souvent pouvoir réaliser des tests de manière automatique, puis revenir le lendemain et parcourir des listings à la recherche de l’erreur.

On peut alors représenter ces arbres de manière préfixe avec un niveau d’indentation qui nous donne la profondeur dans l’arbre, ce qui donnerait pour notre arbre de tout à l’heure :

4 + attributs de la racine
  2 + plein d’informations passionnantes
    1 + là, je raconte ma vie
    3 + là, rien
  7 + coucou c’est moi
    6 + coucou c’est toi
      5 + ici, personne
    8 + mais ici, c’est encore moi

Ceci nous donne beaucoup de place pour visualiser les informations^⁶⁰ relatives à un nœud, sans toutefois cacher la structure inhérente de l’arbre.

Il est donc possible de visualiser des structures complexes, mais pour les graphes, le problème est beaucoup plus grave.

Il y a de nombreuses manières de représenter les données d’un graphe :

la liste des arcs (Ce sont des paires de sommets éventuellement pondérées)
la matrice des connections (tableau indexé par les sommets en ligne et en colonne, avec des booléens ou des poids)
la liste des sommets, munis chacun de la liste des arcs qui en partent.

Pour représenter ces graphes de manière graphique, il y a là un véritable problème de recherche qui n’est pas résolu de manière simple aujourd’hui.

Je conseille de représenter les données brutes. Sinon, on peut toujours représenter tous les sommets en cercle et dessiner des droites les reliant, mais ça n’est pas plus lisible.

Si vous devez vraiment représenter des graphes, je vous souhaite beaucoup de courage.

6.5 La précision et la tolérance d’erreur (numérique)

Il serait illusoire de croire que l’on peut parler de représenter l’information, sans parler de représentation approximative et des erreurs qui en découlent. L’étude des nombres réels nous enseigne même que la plupart d’entre eux ne sont pas représentables du tout. Le nombre  appartient déjà à la classe plus restreinte des nombres que l’on peut représenter de manière finie par l’algorithme qui calcule leurs chiffres (réels récursifs).

Tout ne peut donc pas être représenté de manière exacte. Ce n’est pas un fait surprenant ou rare : tous les ingénieurs qui ont pratiqué la règle à calcul savent qu’ils ont là un outils de calcul d’une précision donnée (qui reste meilleure en général que celle des mesures effectuées).

Même votre montre aussi précise soit-elle, ne vous donne qu’une certaine précision.

6.5.1 Représentation approximative

Le cas de la montre est assez intéressant: il va nous permettre de voir plusieurs problèmes distincts.

L’erreur de départ : Vous avez mis vous-même votre montre à l’heure, par des méthodes manuelles. Elle est donc « à l’heure » plus ou moins les quelques secondes d’imprécision liées à la source et la manipulation.
L’erreur matérielle : Votre montre avance (ou recule) de quelques fractions de seconde quotidiennement.
L’erreur de lecture : Vous savez parfaitement bien lire l’heure. Mais vous arrondissez parfois à la minute ou même à la demi-heure la plus proche.

Ce n’est pas grave pour autant. Vous avez vous même choisi la précision requise.

Lorsque vous cherchez à chronométrer votre pouls, vous choisirez une précision de l’ordre de la seconde, mais quand vous avez besoin de savoir s’il reste plus d’une heure avant le repas, une précision de l’ordre de cinq minutes suffira amplement.

C’est une des raisons pour lesquelles, j’aime la règle à calcul plus que les calculettes. L’utilisateur maîtrise la précision.

Voyons maintenant tout ce que nous perdons dans la représentation des nombres dans un ordinateur.

6.5.1.1 Perte du morphisme pour les entiers

N’ayons pas peur du mot. En permanence, l’esprit humain rapproche des notions maîtrisées sur des objets de types différents.

On se sert couramment de la connaissance d’un objet que l’on projette sur un autre qui lui est semblable. Une fois qu’on sait ouvrir une porte pour sortir d’une chambre, on sait aussi ouvrir une porte pour sortir du salon.

Pour en revenir à notre problème, l’ensemble des nombres entiers relatifs Z est un objet très connu. On imagine à tort, que les entiers de la machine sont équivalents. On fait un « morphisme » des entiers relatifs avec ceux de la machine, croyant alors transmettre toutes les propriétés de Z.

Or, une des propriétés essentielles de Z muni des opérations + et x est que ces opérations sont internes, ce qui signifie que si a et b appartiennent à Z, a+b et axb aussi.

Ce n’est plus vrai dans la machine : la somme de deux entiers de la machine n’est pas forcément représentable dans la machine. Leur produit non plus.

6.5.1.2 Les rationnels décimaux en binaire

Prenons un nombre qui a une représentation exacte, finie et précise : 1/5. Comme 5 est un diviseur de 10, notre base, 1/5 a une représentation finie 0,2.

Mais qu’en est-il en base 2 ? 1/5=0,0011001100110011 avec une jolie période « 0011 ». Donc sa représentation dans une calculatrice va devoir être tronquée. C’est le cas pour de multiples nombres.

Et que devrait rendre une calculatrice à laquelle on demande de nous donner la valeur de 1/3 + 1/3 + 1/3 ? La même erreur a été commise trois fois et pourtant beaucoup de calculatrices répondent quand même 1.

Il existe donc bien un problème de représentation des nombres.

6.5.1.3 Représenter plus ou moins des réels

6.5.1.3.1 Virgules fixes

La première manière de représenter les réels qui est venue à l’esprit des constructeurs d’ordinateurs était la virgule fixe. Les nombres étaient représentés par un entier qui représentait la partie entière et un autre qui représentait la partie fractionnelle.

Les nombres avaient alors une précision fixe, ce qui n’est pas compatible avec une bonne gestion de l’erreur : 2,1234567/10⁸ sera représenté par 2.10^-8 qui n’est connu qu’à travers un chiffre significatif alors que 12345678,12345678 est connu à 10^-16 en relatif.

Une simple division par 1000000 suivie d’une multiplication par 1000000 peut transformer un nombre en n’importe quoi.

6.5.1.3.2 Virgules flottantes

Pour résoudre le problème de la précision relative, on a pensé à représenter les nombres en séparant une partie pour préciser les chiffres significatifs et une autre pour préciser de combien de rang on avait décalé la virgule.

L’intérêt est que nous pouvons maintenant maintenir une erreur relative à peu près constante. Si les nombres a et b sont connus avec une précision relative ε de l’ordre de 10^-8, alors axb est connu à 2ε + ε’ avec ε’ l’erreur relative introduite par la multiplication.

Malheureusement, il y a toujours le problème de la soustraction de deux valeurs du même ordre : si a vaut 1 à ε près et b vaut 1 à ε près, a-b peut aussi bien être positif que négatif. L’erreur relative est infinie.

L’égalité de deux réels calculés par la machine est indécidable. On peut tout aussi bien avoir deux réels distincts qui ont une représentation commune (10¹⁰ et 10¹⁰+1) qu’avoir un réel calculé par deux méthodes différentes qui produisent deux valeurs distinctes.

6.5.2 Gérer l’erreur

Il va être nécessaire d’estimer l’erreur relative.

6.5.2.1 Situons le problème

Prenons un exemple concret de programme où il est nécessaire de comparer des valeurs flottantes : nous programmons un ray-tracer. Ce n’est pas l’objet de cet ouvrage que de rentrer dans les arcanes de l’informatique graphique, mais je peux tout de même préciser de quoi il s’agit.

Pour calculer une image, on lance un rayon fictif qui part de l’œil de l’observateur et qui passe par chacun des pixels de l’écran. On cherche alors si le rayon touche une des formes géométriques de la scène. Si oui, on choisira la figure la plus proche, puis on tentera de voir si le point d’intersection est éclairé ou non et on déterminera la couleur du pixel comme étant la somme de la couleur du point d’intersection, de la couleur du rayon réfléchi et de la couleur du rayon réfracté.

Pour se concentrer sur notre problème, nous venons de calculer un point d’intersection sur une forme. Nous allons ensuite voir si ce point est éclairé par une source lumineuse : nous lançons de nouveau une demi-droite depuis notre source lumineuse cette fois-ci, en direction de notre point d’intersection et nous cherchons le premier point d’impact sur une forme.

Si ce point d’impact est « égal » à notre point d’intersection, alors le point est éclairé.

Si nous programmons la comparaison des deux point avec l’opération = sur les flottants représentant les coordonnées, alors, une figure qui devait être uniformément éclairée se retrouve constellée de petite taches noires.

Ces taches incongrues correspondent à cette imprécision qui fait que le deuxième calcul qui doit aboutir au même point est fait avec d’autres valeurs et il est très courant que le résultat soit différent.

Il ne faut pas regarder si les deux points sont égaux, mais si leur distance est inférieure au pixel, auquel cas ils ont de fortes chances d’être égaux et s’ils ne le sont pas, cela ne se verra pas de toute façon.

6.5.2.2 Estimons l’erreur

De manière plus générale, nous n’avons pas toujours une donnée comme le pixel qui nous permet de majorer assez violemment l’erreur relative. Alors il nous faut donc estimer l’erreur de manière statique.

Nous connaissons l’ordre de grandeur des données que nous manipulons et nous savons combien d’opérations nous leur faisons subir. A chaque opération, nous rajoutons de l’erreur relative.

C’est le moment de factoriser certains calculs et même parfois de changer l’ordre de certaines évaluations pour éviter de sortir des intervalles où les calculs sont corrects.

Puis la comparaison entre les deux représentations flottantes de nos réels se fait en regardant si la valeur absolue de leur différence est inférieure à notre erreur relative.

Si cette différence est supérieure à l’erreur, nous sommes sûr qu’ils sont différents.

Par contre et c’est mathématiquement irrémédiable^⁶¹, si cette valeur est inférieure à l’erreur, nous ne pouvons conclure qu’à la possibilité de l’égalité. En somme, nous conclurons en toute franchise qu’il est possible voire probable selon, que les deux réels représentés soient les mêmes.

6.5.2.3 Alors, en pratique, comment calcule-t-on un sinus ?

Il vous apparaît immédiatement que le calcul des fonctions spéciales de votre calculatrice risquent fort d’être imprécise : nous avons tous fait des développements limités de ces fonctions en imaginant qu’il suffirait de développer à un ordre suffisant pour pouvoir les calculer avec plus de précision.

Mais à partir d’un certain ordre, nous allons rajouter plus d’erreur que nous n’allons rajouter de précision !

En fait, ce n’est pas en développant à l’infini que nous obtenons les bonnes valeurs. Nos calculettes font un peu comme nos ancêtres ingénieurs qui utilisaient des tables de logarithmes.

En pratique, on se ramène à un intervalle connu. Puis on calcule avec un développement limité d’ordre 3 au voisinage du centre de l’intervalle avec des valeurs calculées d’avance.

7 Techniques de développement moderne, l’Extreme Programming

Comme nous avons abordé la méthodologie de programmation dans cet ouvrage, il serait dommage de ne pas glisser un mot sur la conduite de projet.

Les problèmes du développement découlent souvent de problèmes d’organisation externe.

Parfois, on a une équipe de développement qui se met à perdre du temps parce qu’un d’entre eux reçoit tous les jours la visite d’un chef produit issu du marketing qui vient lui donner des consignes qui ont des répercussions sur le travail de chacun des membres.

Cela peut aussi venir du directeur technique qui a une trop bonne idée de ce qu’il faut faire et court-circuite ses chefs de projet pour aller donner des consignes aux responsables de la base de données.

Souvent, cela apparaît dans les structures qui ont trop grandi. Le développeur se retrouve avec un chef pour la qualité, un chef pour les ressources humaines, un chef pour le projet, sans compter les commerciaux qui viennent lui demander des comptes, des explications ou des corrections, le marketing qui ne veut pas perdre son titre de chef produit…

C’est une des meilleurs techniques pour faire capoter un développement : multiplier les chefs. On peut aussi démotiver les troupes en leur montrant combien ils sont nuls. Parmi toutes les techniques éprouvées de destruction de projet, il y a l’adjonction d’un nouveau chef, le licenciement de la secrétaire, les déménagements à répétition, confier le contrôle qualité à quelqu’un de psychorigide, l’obstination à trouver des coupables plutôt que des causes, faire des promesses qui n’engagent que ceux qui y croient, multiplier les réunions en choisissant des ordres du jour très flous voire sans ordre du jour…

La liste est loin d’être exhaustive. Je vous conseille la lecture des ouvrages de Scott Adams (au rayon management de toute bonne librairie) ou une visite quotidienne à son site www.dilbert.com, pour parfaire votre éducation.

Mais cela ne règle pas notre problème. Je n’ai pas trouvé dans Merise de solution pour les problèmes d’aujourd’hui, mais par contre, suite à des exposés sur la méthode DSDM, je me suis intéressé à l’Extreme programming.

Il y a là de quoi améliorer sensiblement nos résultats en matière de génie logiciel.

Un article d’un journal d’informatique français prétendait même que l’Extreme programming était à l’origine de l’amélioration des statistiques de réussites des projets informatiques entre les années 1990 et 2000. En effet, 16% seulement des projets aboutissaient en temps et en heures alors qu’en 2001 nous en étions à 25%.

Vous me direz que cela signifie 75% de projets qui échouent. Malheureusement non. Sur ces trois quarts de non réussite, il n’y en a qu’un pour les échecs propres et nets. Il reste une moitié de projets qui commencent par exploser les limites de leur budget puis prennent du retard. Le problème est qu’on a trop investi pour pouvoir abandonner et compter les pertes.

Il est presque aussi important de savoir s’arrêter que de savoir mener les choses à bien. Nous allons voir ensemble ce qui caractérise l’Extreme programming pour nous en inspirer dans nos futurs projets.

7.1 Petites équipes et échéances courtes

L’expérience nous force à constater qu’une réunion avec plus de cinq participants est souvent plus longue ou plus stérile^⁶². De même, pour une équipe de développement, il faut travailler en petite équipe. Nous allons détailler les rôles essentiels à représenter dans ces équipes par la suite.

D’autre part, il n’est plus acceptable de laisser un projet partir dans un tunnel de plus d’une semaine. Il faut pouvoir ce fixer des objectifs à très court terme avec une démonstration du travail effectué pour que tout le monde sache où on en est.

De l’investisseur au programmeur en passant par le chef de projet, l’utilisateur ou le commercial, tout le monde veut savoir où on en est. D’autre part, le time to market, c’est-à-dire le temps entre le moment où on a l’idée et le moment où il faut que le produit soit sur le marché, est très court (il y a la concurrence, mais il y aussi la durée de vie de l’intérêt du public pour une fonctionnalité).

Bref, il faut aller très vite et il faut pouvoir à chaque instant savoir comment on avance et pouvoir extrapoler la date de livraison et le coût global de l’opération.

En pratique, même un gros projet se retrouve découpé en entités indépendantes pour arriver à faire que chaque projet soit géré par un équipe de quatre à six personnes en six à huit semaines.

Ce sont évidemment des valeurs indicatives. Mon meilleur projet rentrait exactement dans ces limites : nous étions cinq et nous avons fait le travail en deux mois jours pour jours.

Bon, je triche, nous étions en fait trois à travailler et il n’y avait que deux personnes pour nous interrompre avec des questions bêtes. D’ailleurs, nous disposions à l’origine d’un an pour terminer le projet… c’est dire si les échéances devaient être courtes^⁶³.

Tout cela pour bien comprendre qu’un petit nombre de développeur s’impose pour diminuer la perte de temps liée à la coordination des participants.

L’équipe doit quand même comporter d’autres personnes que des développeurs. Il faut en particulier un ambassadeur des utilisateurs, rôle sur lequel je m’appesantirai quelque peu bientôt. Par contre, même s’il n’est pas nécessaire de représenter grandement les départements commerciaux et marketing, il est indispensable qu’une personne du projet leur fasse une démonstration hebdomadaire pour rassembler leurs desiderata et agir en fonction^⁶⁴. Il nous faut aussi une personne pour effectuer les tests, une personne en charge du contrôle des versions et des sauvegardes journalières, hebdomadaires hors site, mais les casquettes sont cumulables.

Je n’ai pas parlé du chef de projet, mais là, il s’agit d’une méthode qui n’a pas été développée en France. Nous pouvons donc isoler une charge de responsable du projet qui pourra tomber sur les épaules de n’importe lequel des intervenants cités au-dessus, qui devra maintenir à jour le diagramme de Gantt du projet. Je choisirais instinctivement la personne qui s’occupe de rendre compte aux commerciaux. Il était conseillé dans les documents que ce rôle soit distribué à une personne différente à chaque projet. Il ne faut pas non plus tomber dans l’excès inverse et donner ce travail à quelqu’un qui déteste ce genre d’activité.

Les échéances courtes correspondent aussi au besoin de pouvoir abandonner rapidement une avenue de développement stérile. En effet, il ne faut pas s’obstiner lorsque le projet se révèle plus complexe qu’au départ. Il faut pouvoir, soit redessiner le diagramme de Gantt en prévenant aussi les investisseurs, soit changer la définition du projet et éventuellement embaucher une équipe supplémentaire pour résoudre le problème que l’on n’avait pas envisagé au début.

Mais cela suppose un grand investissement humain de la part de l’investisseur.

7.2 L’ambassadeur des utilisateurs

C’est le rôle le plus important dans notre équipe. C’est l’utilisateur qui détermine la fonctionnalité à développer. Ce rôle peut être rempli idéalement par un ergonome qui saura déterminer comment rendre une fonctionnalité utilisable.

Dans l’Extreme programming, c’est l’utilisation qui dirige le développement. Une fonctionnalité qui apparaît nécessaire en cours de route devra être intégrée même si elle n’est pas décrite dans un cahier des charges. De même, si on a programmé une fonctionnalité prévue dans le cahier des charges original et qu’à l’usage, on découvre son inutilité, on n’hésitera pas à la faire disparaître du produit final.

Le client est roi. C’est le client qui est ici représenté. La démonstration hebdomadaire est conçue pour lui et parfois par lui. Cette démonstration doit pouvoir servir à diriger le développement, mais aussi pour les commerciaux à trouver des clients prospects ou des partenaires, voire des investisseurs, pour les investisseurs à vérifier que leur argent ne part pas par les fenêtres.

L’ambassadeur des utilisateurs, c’est la garantie d’un produit fonctionnel. Pour travailler, il lui faut prévoir des moyens de décrire ce qu’il veut de manière concrète. Ce n’est souvent pas un développeur. S’il est en contact permanent avec les développeurs, il va falloir qu’à défaut d’un cahier des charges fixe, il leur livre quelque chose d’utilisable pour diriger leur développement.

7.3 Des scénarios d’utilisation plutôt qu’un cahier des charges préliminaire

Pour décrire sa vision du produit, l’utilisateur va dessiner des captures d’écran décrivant les diverses situations dans lesquelles il s’imagine.

Il va décrire de bout en bout l’ensemble d’un scénario d’utilisation afin d’être sur d’isoler toutes les petites fonctionnalités nécessaires. Il va devoir créer un scénario pour chaque type d’utilisateur possible et chaque idée d’utilisation.

C’est un travail fastidieux qui demande beaucoup de rigueur car il faut maintenir ces documents à jour tout au long du projet. Ces documents servent à décrire l’interface utilisateur. Cela doit suffire aux développeurs pour pouvoir avancer, aux testeurs pour pouvoir valider, aux commerciaux pour faire des démonstrations impressionnantes, et à l’investisseur pour dormir tranquille.

7.4 Validation des programmes

Il me semble nécessaire d’ouvrir une section spéciale pour la validation des programmes à l’heure où de nombreux éditeurs de logiciels livrent des versions alpha, se font racheter puis remplacent tous leur développeurs et se retrouvent dans l’incapacité d’effectuer la maintenance ou plus simplement la correction des applications qu’ils ont commises.

Il est quand même possible de livrer des logiciels acceptables avec un minimum de soucis de qualité.

7.4.1 Le passage du prototype à l’application réelle

Il faut dès le départ savoir qu’un prototype n’est pas un logiciel. De nombreux ouvrages estiment le temps nécessaire au passage de l’un à l’autre comme étant deux fois plus long que le temps nécessaire au développement du prototype.

Comme peu d’investisseurs sont près à consacrer ce genre de ressources à un projet, il faut en tant que développeur ou chef de projet de proximité, prendre conscience du fait que l’on est en train de développer du code qui sera très certainement inclus dans la version finale.

On fera donc aussi souvent que possible, les efforts de réécriture qui permettrons de transformer un prototype de module en sa version définitive. Si ce n’est jamais possible, alors on fera un effort maximal de propreté du code et de documentation interne.

Soyons réalistes, personne ne veut payer trois fois plus cher, juste pour ce débarrasser de quelques plaintes de clients qui de toute façon n’ont pas le choix. En conséquence, il faut que le prototype soit le meilleur possible et que sa modularité permette, le cas échéant la réécriture des modules trop fragiles pour une application sérieuse.

7.4.2 Preuve de programme versus tests pratiques

Il existait jadis un métier qui peut sembler curieux aujourd’hui : celui de la preuve de programme. Il fallait par l’étude d’un programme sur le papier, déterminer s’il était sûr d’aboutir correctement.

C'est un travail qui doit changer radicalement. On a aujourd'hui les moyens d'écrire des programmes corrects par construction. C'est le travail du programmeur lui-même, de montrer avant l'écriture, que son programme produit l'effet demandé.

Nous n'en sommes plus à l'age du programme FORTRAN ou des milliers de lignes d’assembleur dont les boucles peuvent ne pas terminer dans les conditions prévues au départ. De plus, nous ne sommes plus contraints par le manque de place mémoire ou par la lenteur des processeurs de ces époques reculées. Il faut maintenant produire vite et bien.

Il est donc prévu de ne pas prouver que le programme est correct mais d’en acquérir la conviction par un ensemble de tests exhaustifs.

Il y a essentiellement deux niveaux de tests pratiques : le test unitaire et le test complet. On confie le premier au programmeur en général. Le test complet est souvent confié à une équipe délocalisée pour qu’elle ne soit pas influencée dans sa méthodologie par l’historique du développement.

Dans la réalité, la preuve de programme permettait de repérer certaines erreurs, mais ne garantissait pas vraiment la perfection. Les tests ne garantissent rien non plus, mais en les multipliant et en les diversifiant, on peut arriver à de très bon taux de détection d’erreur.

C’est un gage de qualité que d’avoir plusieurs méthodologies de tests. Les tests unitaires qui sont conçus avant et pendant la programmation doivent être passés avant toute livraison au logiciel de gestion de version. Les tests du logiciel complet doivent être conçu a priori et complété au fur et à mesure.

L’équipe de test ne doit pas être la seule à tester : les développeurs sont évidemment invités à tester de manière intensive, mais l’utilisateur, les commerciaux et toutes les personnes qui peuvent apporter un point de vue supplémentaire, devraient aussi apporter leur contribution au test.

7.4.3 Tests automatiques et tests manuels

Il se trouve que le travail du test est extrêmement fastidieux et que, surtout pour le test unitaire, il est aussi indispensable qu’il est rébarbatif.

Heureusement, il est souvent possible d’automatiser la plupart des tests unitaires. Les tests d’interface utilisateurs sont plus pénibles à automatiser, mais il existe des outils pour cela (la classe Robot de Java 1.3 par exemple permet de simuler un utilisateur).

Il est de bon goût que le responsable de l’intégration, c'est-à-dire la personne qui va s’occuper de la gestion de version, des sauvegardes et de la coordination entre les projets, ait prévu un passage quotidien de l’ensemble des modules aux tests unitaires.

En effet, lorsqu’on livre un module qui est validé par ces tests, il est possible qu’il y ait une interaction avec d’autres modules qui rendent ceux-ci défectueux. Il faut immédiatement repérer le problème pour éviter les régressions. Il sera alors nécessaire, soit de faire évoluer les autres modules, soit de prévoir une version dépréciée du module en cause (le mot clé deprecated de Java correspond à cette possibilité de garder d’anciennes versions).

Par contre, même si on a réussi à automatiser l’ensemble des tests unitaires, il sera toujours nécessaire de passer l’épreuve de l’utilisateur réel. Il y aura toujours une manipulation du logiciel à laquelle on n’aura pas pensée et qui sera découverte par le premier testeur humain venu.

7.4.4 Le cahier des charges final et la recette

Pour gagner de l’argent, il est en général nécessaire de livrer quelque chose qui a été prévu par contrat. Il nous faudrait donc savoir au moment de la signature du contrat, quelles sont les fonctionnalités exactes que l’on va livrer.

J’ai pourtant insisté longuement pour expliquer que ce n’est plus possible, mais on me demande un cahier des charges initial. Il faut donc réaliser un cahier des charges, sous la forme de la liste de scénarios dont nous parlions, puis la faire évoluer avec l’accord des contractants pendant toute la durée du développement.

Ainsi, lors de la recette finale, il y aura effectivement un document correspondant, d’une part à ce qui a été réalisé et d’autre part, à ce qui était nécessaire.

Maintenant, pour du développement de logiciel, il n’est concevable de faire des contrats forfaitaires avec des clauses de pénalité non libératoires que lorsqu’on est une entreprise très solide. Je conseillerais plutôt des contrats de régie avec des objectifs de courte durée pour faire le développement sur place, au contact des utilisateurs.

On me répondra qu’il est plus économique de faire développer le même logiciel dans un pays lointain où la main d’œuvre est moins chère, mais on est alors obligé de revenir à des schémas de développement classique avec des cahiers des charges figés. On reçoit alors souvent ce qu’on a demandé, mais beaucoup plus rarement ce qu’on voulait.

7.5 La gestion de version

Je connais des directeurs de projets qui sont en faveur de la gestion manuelle des différentes versions des modules d’un logiciel. Ayant une expérience des logiciels RCS, SCCS, CVS et WinCVS, je préfère que ce soit la machine qui s’occupe de nommer les différentes versions. Je me contente de graver un CD toutes les semaines et de l’emmener au coffre fort.

Il est possible avec ces logiciels d’archiver toutes les modifications de chacun des fichiers qui composent un développement logiciel : les fichiers source, les fichiers de spécification, les documents commerciaux, les comptes rendus, les diagrammes de Gantt etc.

Il est ainsi possible à tout instant d’observer l’historique des modifications d’un module. On peut aussi, lorsqu’on découvre une erreur, de trouver à partir de quelle version de quel module elle est apparue. Il sera ainsi possible de déterminer avec quelle modification elle est née.

Lorsqu’on a livré des versions différentes à des clients, il est indispensable de pouvoir régénérer la version de chacun afin de résoudre les problèmes qu’ils ne manqueront pas de signaler.

En conclusion, je conseille d’utiliser un de ces logiciels, de prévoir un passage automatique quotidien aux tests unitaires, de graver des CD avec le contenu du repository du logiciel et de faire des sauvegardes hors site^⁶⁵ (par exemple au coffre fort).

Et c'est fini.

1 Moi en l’occurrence.

2 C’est-à-dire après beaucoup de sang des vaincus i.e. la sélection naturelle.

3 L’homme qui croit qu’il pense qu’il sait ou quelque chose dans ce goût-là.

4 Ainsi que le four micro-onde et bien d’autres signes de sa supériorité incontestable sur l’homme qui ne sait pas qu’il pense, mais ce n’est pas notre propos.

5 Vous remarquerez que je ne cite absolument personne et que je ne fais aucune référence à un quelconque système d’exploitation ou même à des logiciels. Ils détiennent mes données en otage.

6 Dans un millénaire, si un Champollion de l’informatique fait des fouilles, j’espère qu’il ne mourra pas de rire à la vue de nos travaux.

7 Et le titre, à peu de choses près…

8 Ce qui tendrait à prouver que j’en ai au moins lu la préface, ce qui n’est pas le cas pour beaucoup d’autres livres qu’il m’arrive de citer sans les avoir lus.

9 Je préfère le mot « interprète » qui est français depuis toujours au mot « interpréteur » qui ne l’est que depuis peu. Et puis j’ai le droit d’être snob, non ?

10 Ca me fait évidemment très plaisir parce que j’ai écrit beaucoup d’interprètes et de compilateurs et comme beaucoup, je me prends pour un grand maître.

11 Quoi Que Cela Veuille Dire.

12 J’ai honte : je l’ai acheté, feuilleté, mais pas vraiment lu…

13 C’est la partie sadique.

14 « Faites comme je dis, pas comme je fais ! »

15 Surtout, essayer à l’écart de tous les autres singes.

16 Avec une grande lâcheté, je l’avoue, mais je ne débogue plus depuis longtemps.

17 A partir de maintenant j’écrirai « scénarios », mais je n’ai pas résisté à l’envie d’écrire « scénarii » qui fait très prétentieux. J’ai le droit d’être snob.

18 De l’utilisateur vers la machine et non le contraire comme pour les cas historiques nommés ci-dessus.

19 Non, je n’ai pas fini de régler mes comptes avec Marie Claude.

20 Oui, en effet, c’est le même titre ! Vous aviez remarquez. Mais ce n’est pas du tout le même livre. Celui de Aho Hopcroft et Ullman reste une référence incontournable à garder dans toute bonne bibliothèque informatique, là où l’autre peut figurer à titre humoristique.

21 Nous ne modéliserons pas la file d’attente au télésiège qui a un bug célèbre qui porte le nom « ESF priorité 1 sur 2 », cause de nombreuses altercations entre des gens à peu près normaux et des clowns en costume fluo.

22 A part les files prioritaires pour les femmes enceintes, les titulaires de la carte de priorité locale ou autres cousins du patron.

23 Ce qui ne m’est pas arrivé depuis près de trente ans ! Aussi loin que je me souvienne.

24 Puisque je vous le dis !

25 Là, d’un seul coup, ça fait très rigoureux n’est-ce pas ?

26 Par exemple, Rationnal Rose génère le code Java correspondant à un diagramme UML.

27 Une technique utilisée dans l’art de la compilation ou de manière générale pour tous les calculs dirigés par la syntaxe.

28 Ceux-ci croient, après avoir mis dix ans à maîtriser la programmation dans un langage, qu’il leur faudrait plus de dix jours pour en comprendre un autre. Un ami linguiste m’a dit en parlant de langues étrangères qu’à partir de la sixième, il ne lui faut plus que trois semaines pour assimiler une langue au point de pouvoir lire le journal. En informatique, par contre, c’est au bout du deuxième langage que l’on découvre qu’au delà du « sucre syntaxique », tous les langages se ressemblent. Le passage de l’impératif au fonctionnel ou à l’objet peut toutefois être difficile, mais, là ce n’est même plus une question de temps. C’est évidemment une opinion personnelle : Marianne Belis n’est pas du tout d’accord. Elle explique en effet que programmer en Prolog ou en C est tellement différent que connaître l’un n’aide pas pour l’autre.

29 Je n’évoquerai que les dmacro (écrasantes) pour lesquelles les traductions sont faites une fois pour toute, à la première évaluation.

30 Si a est plus petit que b alors (< a b) vaut t et donc l’expression rendue est b, sinon c’est a.

31 Il suffira de remplacer return(<expr>) par <nom de la fonction>:=<expr>.

32 Il suffira de les transformer en deux if imbriqués pour pouvoir les évaluer dans un Pascal plus standard. Si c’est dans l’argument d’un while, faites une petite fonction booléenne.

33 Sachez bien que pour cacher de l’information, on peut ne pas la donner évidemment, mais on peut aussi l’enfouir dans une masse d’autres informations qui ne servent à rien.

34 J’ai une opinion relativement négative de cette norme, mais comme elle est vraiment respectée par l’ensemble de la communauté des programmeurs Java, c’est un plaisir pour moi que de m’y plier.

35Certes, il est possible que vous perdiez des quarts de microcycles, si vous implantez vraiment une récurrence dans le produit final, mais vous aurez divisé par vingt le temps de conception, vous aurez de grandes facilités à expliquer votre algorithme, et votre prototype fonctionnera dès son implantation. D’autre part, une fois le prototype au point, il est facile de le dérécursiver si cela s’avère nécessaire.

36 Vous voyez l’abus de langage et ses conséquences ! Le programmeur croit qu’elle suffit à tout décrire.

37 C’est très rassurant, mais c’est comme ça pour tous les exemples que je vous donne : je vous assure qu’ils fonctionnent parfaitement. Maintenant, si ça pouvait être pareil quand vous les programmez effectivement, je serais le premier surpris.

38 Représentée avec des tableaux.

39 Avec des structures de cellules et des pointeurs. D’où une allocation dynamique de la mémoire.

40 Centaur, le produit successeur de Mentor produit dans les années 80 par le projet Croap de l’INRIA utilisait un manipulateur d’arbres appelé VTP (virtual tree processor) qui manipulait d’abord des arbres représentés avec une structure de listes en Lisp. Il a été réécrit sous forme d’une gigantesque table de hachage des chemins d’accès développée en C. Les manipulations et les parcours n’ont pas étés touchés. Le changement fut entièrement transparent pour les développeurs des couches supérieurs. La seule différence était l’accélération phénoménale de tous les traitements. C’est vraiment un cas d’école de prototypage et d’optimisation réussie.

41 Nous avons quand même choisi quelqu’un qui savait compter, mais avec un mécanisme de bananes et de douches froides, il est peut-être possible d’utiliser un de nos chimpanzés rescapés de l’expérience de l’escabeau.

42 En effet, le calcul est une suite d’additions de la valeur 1 et 10⁸ + 1 est arrondi à 10⁸.

43 Lors de l’exécution du programme, il s’entend.

44 Mais comme on me le répète souvent, la peur n’évite pas le danger.

45 Le choix du paradigme fonctionnel par rapport à l’impératif.

46 Le compte est bon.

47 La version officielle fait une alternance de Min et de Max, d’où le nom. Je préfère coder –Max et avoir deux fois moins de code, donc deux fois moins de bug.

48 Comme Skippy, le grand gourou.

49 Il s’agit de créer un masque sur 30 valeurs où l’on a éliminé tous les multiples de 2, 3 et 5.

50 Ce n’est pas nécessaire pour Java. Tous les types de base sont implémentés et toutes les classes dérivées de Vector peuvent être parcourues avec la classe Iterator.

51 On rend une référence à la cellule contenant sa première occurrence.

52 La recherche est linéaire et nécessite toujours n opérations lors d’un échec, mais rajouter un élément ne nécessite qu’une seule opération.

53 Personnellement, ça me laisse à 37°.

54 La complexité du tri fusion est de l’ordre de n log(n) opérations avec une profondeur de log(n) dans la pile d’évaluation.

55 Ce qui est clairement vrai, mais qui n’était pas nécessaire pour le tri par insertion.

56 L’insertion à la racine est un très bon exercice d’école : c’est compliqué et ça ne sert à rien.

57 Encore une fois, nous nous trouvons dans le cas des 90/10 : nous passons 90% de notre temps et de notre code pour régler 10% des cas. Inversement, 10% de notre code sert au cas général.

58 11, 101, 1001, 10001 n’est pas une famille de nombres premiers, mais ces nombres sont suffisamment peu divisibles pour ne pas présenter d’effet de résonance.

59 L’arithmétique des pointeurs est une chose qu’il était essentiel de faire disparaître dans les langages de haut niveau. Ainsi, cela a disparu de Java ainsi que de C#, mais c’est encore possible en C, alors j’en profite.

60 Passionnantes et pertinentes, il faut le dire.

61 C’est un problème indécidable.

62 De même, dans un couple, dès qu’il y a des amants et des maîtresses, on voit surgir de nombreux problèmes d’organisation. Il faut penser à éteindre son portable, trouver un bon alibi etc.

63 Non, là c’est de l’humour.

64 Justement non, il ne s’agit pas de les mettre à la poubelle ! Je commence à vous connaître.

65 Il y a l’incendie et le dégât des eaux, il y a le vandalisme et les méchants de la concurrence, il y a les disques durs qui meurent, mais il y a aussi les erreurs humaines…